Page 421 - Microeconomics, Fourth Edition

c10competitive markets applications.qxd 7/15/10 4:58 PM Page 395

10.1 THE INVISIBLE HAND, EXCISE TAXES, AND SUBSIDIES 395

S + $10
S + $10
S
$38 S
Price (dollars per unit) $30 Case 1: Price (dollars per unit) $32
$30
$28
Demand is relatively
inelastic compared
$22
with supply
Case 2: D
Supply is relatively
inelastic compared
D
with demand
Quantity with Quantity Quantity with Quantity
no tax no tax
(a) Quantity with tax (b) Quantity with tax
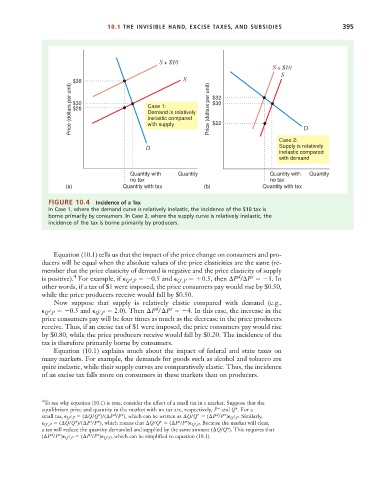
FIGURE 10.4 Incidence of a Tax
In Case 1, where the demand curve is relatively inelastic, the incidence of the $10 tax is
borne primarily by consumers. In Case 2, where the supply curve is relatively inelastic, the
incidence of the tax is borne primarily by producers.

Equation (10.1) tells us that the impact of the price change on consumers and pro-
ducers will be equal when the absolute values of the price elasticities are the same (re-
member that the price elasticity of demand is negative and the price elasticity of supply
4
d
s
s 0.5,
is positive). For example, if Q ,P and Q ,P then P / P 1. In
d 0.5
other words, if a tax of $1 were imposed, the price consumers pay would rise by $0.50,
while the price producers receive would fall by $0.50.
Now suppose that supply is relatively elastic compared with demand (e.g.,
d
s
Q ,P 0.5 and Q ,P 2.0). Then ¢P /¢P 4. In this case, the increase in the
d
s
price consumers pay will be four times as much as the decrease in the price producers
receive. Thus, if an excise tax of $1 were imposed, the price consumers pay would rise
by $0.80, while the price producers receive would fall by $0.20. The incidence of the
tax is therefore primarily borne by consumers.
Equation (10.1) explains much about the impact of federal and state taxes on
many markets. For example, the demands for goods such as alcohol and tobacco are
quite inelastic, while their supply curves are comparatively elastic. Thus, the incidence
of an excise tax falls more on consumers in these markets than on producers.

4 To see why equation (10.1) is true, consider the effect of a small tax in a market. Suppose that the
equilibrium price and quantity in the market with no tax are, respectively, P* and Q*. For a
d
d
small tax, Q ,P (¢Q/Q*)/(¢P /P*), which can be written as ¢Q/Q* (¢P /P*) Q ,P . Similarly,
d
d
s
s
Q ,P (¢Q/Q*)/(¢P /P*), which means that ¢Q/Q* (¢P /P*) Q ,P . Because the market will clear,
s
s
a tax will reduce the quantity demanded and supplied by the same amount (¢Q/Q*). This requires that
d
s
(¢P /P*) Q ,P (¢P /P*) Q ,P , which can be simplified to equation (10.1).
s
d