Page 642 - Microeconomics, Fourth Edition

c15riskandinformation.qxd 8/16/10 11:10 AM Page 616

616 CHAPTER 15 RISK AND INFORMATION

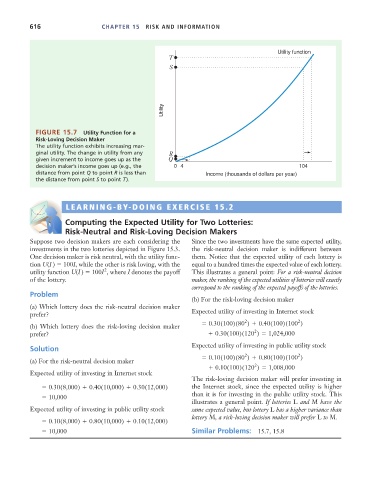
Utility function
T
S

Utility

FIGURE 15.7 Utility Function for a
Risk-Loving Decision Maker
The utility function exhibits increasing mar-
ginal utility. The change in utility from any R
given increment to income goes up as the Q
decision maker’s income goes up (e.g., the 0 4 104
distance from point Q to point R is less than Income (thousands of dollars per year)
the distance from point S to point T).

LEARNING-BY-DOING EXERCISE 15.2
S
D
E
Computing the Expected Utility for Two Lotteries:
Risk-Neutral and Risk-Loving Decision Makers
Suppose two decision makers are each considering the Since the two investments have the same expected utility,
investments in the two lotteries depicted in Figure 15.3. the risk-neutral decision maker is indifferent between
One decision maker is risk neutral, with the utility func- them. Notice that the expected utility of each lottery is
tion U(I ) 100I, while the other is risk loving, with the equal to a hundred times the expected value of each lottery.
2
utility function U(I ) 100I , where I denotes the payoff This illustrates a general point: For a risk-neutral decision
of the lottery. maker, the ranking of the expected utilities of lotteries will exactly
correspond to the ranking of the expected payoffs of the lotteries.
Problem
(b) For the risk-loving decision maker
(a) Which lottery does the risk-neutral decision maker
Expected utility of investing in Internet stock
prefer?
2
2
0.30(100)(80 ) 0.40(100)(100 )
(b) Which lottery does the risk-loving decision maker
2
prefer? 0.30(100)(120 ) 1,024,000
Expected utility of investing in public utility stock
Solution
2
2
0.10(100)(80 ) 0.80(100)(100 )
(a) For the risk-neutral decision maker
2
0.10(100)(120 ) 1,008,000
Expected utility of investing in Internet stock
The risk-loving decision maker will prefer investing in
0.30(8,000) 0.40(10,000) 0.30(12,000) the Internet stock, since the expected utility is higher
than it is for investing in the public utility stock. This
10,000
illustrates a general point. If lotteries L and M have the
Expected utility of investing in public utility stock same expected value, but lottery L has a higher variance than
lottery M, a risk-loving decision maker will prefer L to M.
0.10(8,000) 0.80(10,000) 0.10(12,000)
10,000 Similar Problems: 15.7, 15.8