Page 644 - Microeconomics, Fourth Edition

c15riskandinformation.qxd 8/16/10 11:10 AM Page 618

618 CHAPTER 15 RISK AND INFORMATION
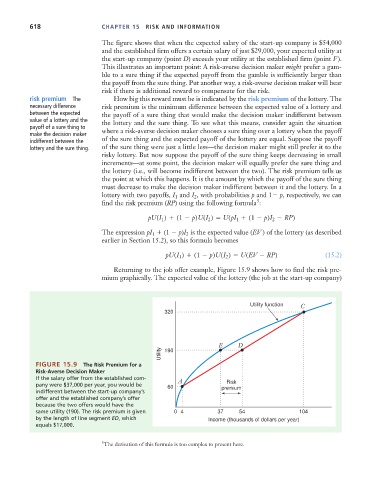
The figure shows that when the expected salary of the start-up company is $54,000
and the established firm offers a certain salary of just $29,000, your expected utility at
the start-up company (point D) exceeds your utility at the established firm (point F).
This illustrates an important point: A risk-averse decision maker might prefer a gam-
ble to a sure thing if the expected payoff from the gamble is sufficiently larger than
the payoff from the sure thing. Put another way, a risk-averse decision maker will bear
risk if there is additional reward to compensate for the risk.
risk premium The How big this reward must be is indicated by the risk premium of the lottery. The
necessary difference risk premium is the minimum difference between the expected value of a lottery and
between the expected the payoff of a sure thing that would make the decision maker indifferent between
value of a lottery and the the lottery and the sure thing. To see what this means, consider again the situation
payoff of a sure thing to where a risk-averse decision maker chooses a sure thing over a lottery when the payoff
make the decision maker
indifferent between the of the sure thing and the expected payoff of the lottery are equal. Suppose the payoff
lottery and the sure thing. of the sure thing were just a little less—the decision maker might still prefer it to the
risky lottery. But now suppose the payoff of the sure thing keeps decreasing in small
increments—at some point, the decision maker will equally prefer the sure thing and
the lottery (i.e., will become indifferent between the two). The risk premium tells us
the point at which this happens. It is the amount by which the payoff of the sure thing
must decrease to make the decision maker indifferent between it and the lottery. In a
lottery with two payoffs, I and I , with probabilities p and 1 p, respectively, we can
1
2
3
find the risk premium (RP) using the following formula :
pU(I ) (1 p)U(I ) U(pI (1 p)I RP)
2
1
2
1
The expression pI (1 p)I is the expected value (EV ) of the lottery (as described
1
2
earlier in Section 15.2), so this formula becomes
pU(I ) (1 p)U(I ) U(EV RP) (15.2)
1
2
Returning to the job offer example, Figure 15.9 shows how to find the risk pre-
mium graphically. The expected value of the lottery (the job at the start-up company)

Utility function C
320

E D
Utility 190

FIGURE 15.9 The Risk Premium for a
Risk-Averse Decision Maker
If the salary offer from the established com- A
Risk
pany were $37,000 per year, you would be 60 premium
indifferent between the start-up company’s
offer and the established company’s offer
because the two offers would have the
same utility (190). The risk premium is given 04 37 54 104
by the length of line segment ED, which Income (thousands of dollars per year)
equals $17,000.

3 The derivation of this formula is too complex to present here.