Page 639 - Microeconomics, Fourth Edition

c15riskandinformation.qxd 8/16/10 11:10 AM Page 613

15.2 EVALUATING RISKY OUTCOMES 613

Utility
C function
320
Upside
of lottery
B
230
Utility Downside 190 D
of lottery

A
60

0 4 54 104
Income (thousands of dollars per year)

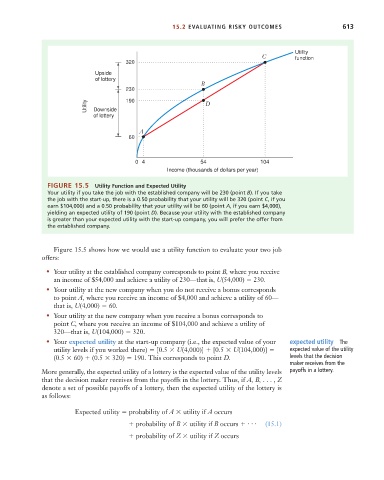
FIGURE 15.5 Utility Function and Expected Utility
Your utility if you take the job with the established company will be 230 (point B). If you take
the job with the start-up, there is a 0.50 probability that your utility will be 320 (point C, if you
earn $104,000) and a 0.50 probability that your utility will be 60 (point A, if you earn $4,000),
yielding an expected utility of 190 (point D). Because your utility with the established company
is greater than your expected utility with the start-up company, you will prefer the offer from
the established company.

Figure 15.5 shows how we would use a utility function to evaluate your two job
offers:
• Your utility at the established company corresponds to point B, where you receive
an income of $54,000 and achieve a utility of 230—that is, U(54,000) 230.
• Your utility at the new company when you do not receive a bonus corresponds
to point A, where you receive an income of $4,000 and achieve a utility of 60—
that is, U(4,000) 60.
• Your utility at the new company when you receive a bonus corresponds to
point C, where you receive an income of $104,000 and achieve a utility of
320—that is, U(104,000) 320.
• Your expected utility at the start-up company (i.e., the expected value of your expected utility The
utility levels if you worked there) [0.5 U(4,000)] [0.5 U(104,000)] expected value of the utility
(0.5 60) (0.5 320) 190. This corresponds to point D. levels that the decision
maker receives from the
More generally, the expected utility of a lottery is the expected value of the utility levels payoffs in a lottery.
that the decision maker receives from the payoffs in the lottery. Thus, if A, B, . . . , Z
denote a set of possible payoffs of a lottery, then the expected utility of the lottery is
as follows:

Expected utility probability of A utility if A occurs
probability of B utility if B occurs . . . (15.1)
probability of Z utility if Z occurs