Page 661 - Microeconomics, Fourth Edition

c15riskandinformation.qxd 8/16/10 11:10 AM Page 635

15.5 AUCTIONS 635
AUCTIONS WHEN BIDDERS HAVE PRIVATE VALUES

To study bidding behavior in auctions, let’s first consider a setting in which bidders
have private values. We will explore three different auction formats: the first-price
sealed-bid auction, the English auction, and the second-price sealed-bid auction. Our
goals are to see how the rules of an auction affect the behavior of bidders and to see
how much revenue auctions raise for sellers.

First-Price Sealed-Bid Auctions
Suppose you and other bidders are competing to purchase an antique dining room
table that is being offered for sale on eBay. Also suppose (1) that this table is worth
$1,000 to you—that is, the most you are willing to spend to buy this table is $1,000,
(2) that you do not know the valuations of other potential bidders, and (3) that you
believe that some bidders could have valuations above or below $1,000.
In deciding on a bidding strategy, it might seem natural to submit a bid of $1,000.
After all, that is what the table is worth to you, and by bidding as high as possible, you
maximize your chances of winning. However, this is generally not your best strategy.
In a first-price sealed-bid auction, a bidder’s optimal strategy is to submit a bid that is
less than the bidder’s maximum willingness to pay.
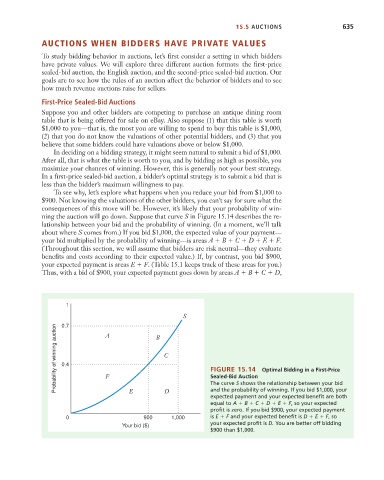
To see why, let’s explore what happens when you reduce your bid from $1,000 to
$900. Not knowing the valuations of the other bidders, you can’t say for sure what the
consequences of this move will be. However, it’s likely that your probability of win-
ning the auction will go down. Suppose that curve S in Figure 15.14 describes the re-
lationship between your bid and the probability of winning. (In a moment, we’ll talk
about where S comes from.) If you bid $1,000, the expected value of your payment—
your bid multiplied by the probability of winning—is areas A B C D E F.
(Throughout this section, we will assume that bidders are risk neutral—they evaluate
benefits and costs according to their expected value.) If, by contrast, you bid $900,
your expected payment is areas E F. (Table 15.1 keeps track of these areas for you.)
Thus, with a bid of $900, your expected payment goes down by areas A B C D,

1
S
Probability of winning auction 0.4 F C FIGURE 15.14 Optimal Bidding in a First-Price
0.7
A
B

Sealed-Bid Auction
The curve S shows the relationship between your bid
and the probability of winning. If you bid $1,000, your
E
D
expected payment and your expected benefit are both
equal to A B C D E F, so your expected
profit is zero. If you bid $900, your expected payment
0 900 1,000 is E F and your expected benefit is D E F, so
your expected profit is D. You are better off bidding
Your bid ($)
$900 than $1,000.