Page 665 - Microeconomics, Fourth Edition

c15riskandinformation.qxd 8/16/10 11:10 AM Page 639

15.5 AUCTIONS 639
bidders have private values and each bidder follows the Nash equilibrium strategy, the
bidder with the highest willingness to pay wins the auction. We have also seen that:

• In a first-price sealed-bid auction, the winning bidder pays a price that is less
than his or her maximum willingness to pay.
• In an English auction and in a second-price sealed-bid auction, the winning
bidder pays a price that is equal to the second-highest private valuation among
all the bidders in the auction.

Thus, each format successfully identifies the bidder with the highest valuation, but the
seller’s revenue (the winning bid) is less than that highest valuation. Remarkably, the
seller’s revenue in English and second-price sealed-bid auctions—the second-highest
private valuation among all the bidders in the auction—is also the seller’s revenue in
first-price sealed-bid auctions and in all other types of auctions when bidders have private
values and follow Nash equilibrium strategies. This surprising result (which is too com-
plex to derive here) is called the revenue equivalence theorem: When bidders have revenue equivalence
private values, all auction formats generate the same revenue for the seller, equal on theorem When partici-
average to the second-highest private valuation among all the bidders in the auction. pants in an auction have
private values, any auction
format will, on average,
AUCTIONS WHEN BIDDERS HAVE COMMON VALUES: generate the same revenue
THE WINNER’S CURSE for the seller.
When bidders have common values, a complication arises that does not occur when
bidders have private values, the winner’s curse: The winning bidder might bid an winner’s curse A
amount that exceeds the item’s intrinsic value. To see how this can happen, suppose phenomenon whereby
your economics professor brings a briefcase full of dollar bills to class and auctions it the winning bidder in a
off. Every student is given a peek inside the briefcase to estimate how much it con- common-values auction
tains. You estimate that it contains $150, which represents the most you would be will- might bid an amount
that exceeds the item’s
ing to bid. Of course, your classmates develop their own estimates, and these might intrinsic value.
differ from yours. Let’s suppose that these estimates are distributed according to the
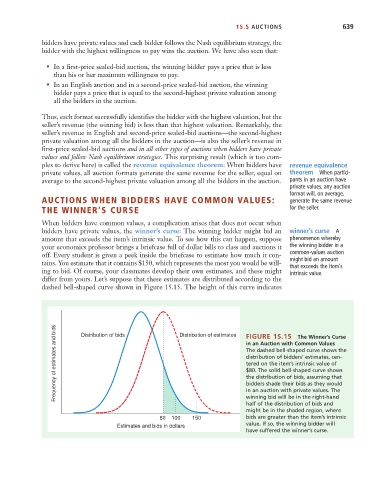
dashed bell-shaped curve shown in Figure 15.15. The height of this curve indicates

Frequency of estimates and bids Distribution of bids Distribution of estimates FIGURE 15.15 The Winner’s Curse

in an Auction with Common Values
The dashed bell-shaped curve shows the
distribution of bidders’ estimates, cen-
tered on the item’s intrinsic value of
$80. The solid bell-shaped curve shows
the distribution of bids, assuming that
bidders shade their bids as they would
in an auction with private values. The
winning bid will be in the right-hand
half of the distribution of bids and
might be in the shaded region, where
80 100 150 bids are greater than the item’s intrinsic
value. If so, the winning bidder will
Estimates and bids in dollars
have suffered the winner’s curse.