Page 141 - Fiber Optic Communications Fund

122 Fiber Optic Communications

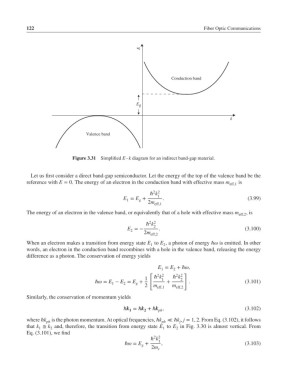
E

Conduction band

E g

k

Valence band

Figure 3.31 Simplified E–k diagram for an indirect band-gap material.

Let us first consider a direct band-gap semiconductor. Let the energy of the top of the valence band be the
reference with E = 0. The energy of an electron in the conduction band with effective mass m is
eff,1
2 2
ℏ k 1
E = E + . (3.99)
g
1
2m eff,1
The energy of an electron in the valence band, or equivalently that of a hole with effective mass m eff,2 ,is
2 2
ℏ k 2
E =− . (3.100)
2
2m
eff,2
When an electron makes a transition from energy state E to E , a photon of energy ℏ is emitted. In other
2
1
words, an electron in the conduction band recombines with a hole in the valence band, releasing the energy
difference as a photon. The conservation of energy yields
E = E + ℏ,
1 2
[ 2 2 2 2 ]
1 ℏ k 1 ℏ k 2
ℏ = E − E = E + + . (3.101)
1
g
2
2 m eff,1 m eff,2
Similarly, the conservation of momentum yields
ℏk = ℏk + ℏk , (3.102)

ph
where ℏk is the photon momentum. At optical frequencies, ℏk ph ≪ℏk , j = 1, 2. From Eq. (3.102), it follows
ph
j
that k ≅ k and, therefore, the transition from energy state E to E in Fig. 3.30 is almost vertical. From
1
2
1
2
Eq. (3.101), we find
2 2
ℏ k 1
ℏ = E + , (3.103)
g
2m
r