Page 33 - CCFA Journal - Fourth Issue
P. 33
加中金融 Quant Corner 数量分析
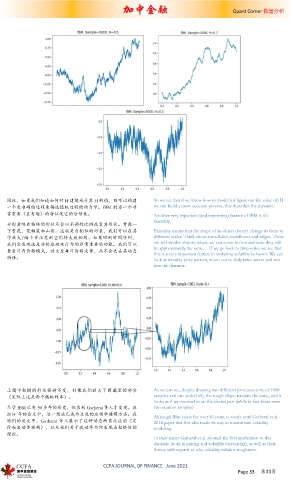
因此,如果我们知道如何对 H 建模或计算 H 的值,则可以构建 So we see that if we know how to model (or figure out the value of) H
一个更准确的过程来描述随机过程的动力学。fBM 的另一个非 we can build a more accurate process, that describes the dynamic.
常重要(且有趣)的特征是它的分形性。 Another very important (and interesting) feature of fBM is it’s
fractality.
分形意味着物体的形状不会以不同的比例改变其形状。考虑一
下雪花,花椰菜和山脊。这些是自相似的对象,我们可以在其 Fractality means that the shape of an object doesn’t change its form at
中放大/缩小并注意到它们将大致相同。如果回到时间序列, different scales. Think about snowflakes, cauliflower and ridges. These
are self-similar objects, where we can zoom in/out and note they will
我们会发现这是分析波动性行为的非常重要的功能。我们可以
be approximately the same… If we go back to time-series we see that
查看日内价格模式,放大至每日价格走势,而不会失去其动态 this is a very important feature in analyzing volatility behavior. We can
特性。 look at intraday price pattern, zoom out to daily price action and not
lose the dynamic.
上图中粗糙的形状保持不变,好像我们放大了圆圈里的部分 As we can see, despite drawing two different processes (one of 1000
(实际上这是两个随机样本)。 samples and one scaled x5), the rough shape remains the same, and it
looks as if we zoomed in on the circled part (while in fact these were
尽管 fBM 已有 50 多年的历史,但直到 Gatheral 等人才发现。在 two random samples)
2014 年的论文中,这一想法已成为主流的波动率建模方法。在
Although fBm exists for over 50 years, it wasn’t until Gatheral et al.
他们的论文中,Gatheral 等人展示了这种动态的首次应用(定 2014 paper that this idea made its way to mainstream volatility
价和波动率预测),以及他们关于波动率为何表现出粗糙性的 modeling.
理论。
In their paper Gatheral et al. showed the first application to this
dynamic (both in pricing and volatility forecasting), as well as their
theory with regards to why volatility exhibits roughness.
CCFA JOURNAL OF FINANCE June 2021
Page 33 第33页