Page 256 - FUNDAMENTALS OF COMPUTER

256 Fundamentals of Computers NPP

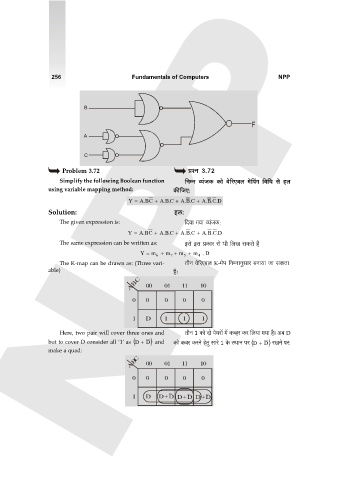
B
F

A

C

Problem 3.72 àíZ 3.72

Simplify the following Boolean function {ZåZ ì`§OH$ H$mo do[aE~b _oqnJ {d{Y go hb
using variable mapping method: H$s{OE:
Y = B . A C + C . B . A + C . B . A + D . C . B . A
Solution: NPP hc:

The given expression is: {X`m J`m ì`§OH$
Y = B . A C + C . B . A + C . B . A + D . C . B . A
The same expression can be written as: Bgo Bg àH$ma go ^r {bI gH$Vo h¢

Y = m + m + m + m 4 . D
5
6
7
The K-map can be drawn as: (Three vari- VrZ do[aE~b K-_on {ZåZmZwgma ~Zm`m Om gH$Vm
able) h¡…
A B .C 00 01 11 10

0 0 0 0 0

1 D 1 1 1

Here, two pair will cover three ones and VrZ 1 H$mo Xmo no`am| _| H$ìha H$a {b`m J`m h¡& A~ D
but to cover D consider all ‘1’ as (D + D ) and H$mo H$da H$aZo hoVw gmao 1 Ho$ ñWmZ na (D + D ) aIZo na:
make a quad:
A B C 00 01 11 10

0 0 0 0 0

1 D D + D D + D D + D