Page 50 - E-MODUL- Aplikasi Turunan dengan Pendekatan RME Berbasis Pemecahan Masalah Polya

Sekarang kita membuat suatu pengamatan penting. Jika kita ketahui bahwa terdapat

suatu bilang c dalam ( , ) yang memenuhi ( ) = 0. Kita akan selesai. Karena persamaan
′
yang terakhir mengatakan bahwa yang setara terhadap kesimpulan teorema tersebut.

( ) − ( )
′
0 = ( ) −
−
′
Untuk melihat bahwa ( ) = 0 untuk suatu dalam ( , ), alasannya sebagai berikut.
Jelas kontinu pada [ , ], karena merupakan selisih dua fungsi kotinu. Jadi menurut teorema
keberadaaan maks-min (teorema 3.1A), harus mencapai baik nilai maksimum ataupun nilai

minimum pada [ , ]. Jika kedua nilai ini kebetulan adalah 0, maka ( ) secara identic adalah

′
0 pada [ , ], akibatnya ( ) = 0 untuk smeua x dalam ( , ), jauh lebih banyak dari pada
yang kita perlukan.

Jika salah satu nilai maksimum atau nilai minimum berlainan dengan 0, maka nilai

tersebut dicapai pada sebuah titik dalam , karena ( ) = ( ) = 0. Sekarang mempunyai
′
turunan disetiap titik dari ( , ), sehingga menurut teorema titik kritis (teorema 3.1B). ( ) =
0. Itulah semua yang kita perlukan untuk diketahui.

Kunci terhadap Bukti

Kunci terhadap bukti ini adalah bahwa c
′
adalah nilai tempat ( ) =
( )− ( ) ′
( ) = 0. Banyak
−
bukti mempunyai satu atau dua
gagasan kunci, jika anda memahami
kunci tersebut anda akan
memahami bukti .

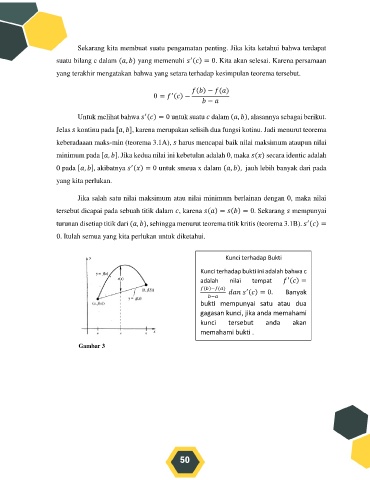
Gambar 3

50