Page 10 - E-Book - Fungsi Eksponen-

FUNGSI EKSPONEN | # MATEMATIKA PEMINATAN #

D. Penerapan Fungsi Eksponen

 Pertumbuhan (Pertambahan )

Pada pembahasan sebelumnya, kita telah mengetahui grafik fungsi eksponen ( ) =

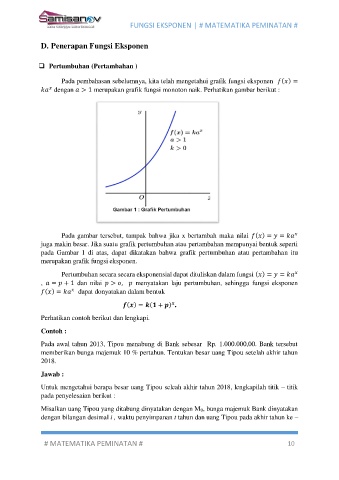
dengan > 1 merupakan grafik fungsi monoton naik. Perhatikan gambar berikut :

Pada gambar tersebut, tampak bahwa jika x bertambah maka nilai ( ) = =

juga makin besar. Jika suatu grafik pertumbuhan atau pertambahan mempunyai bentuk seperti
pada Gambar 1 di atas, dapat dikatakan bahwa grafik pertumbuhan atau pertambahan itu
merupakan grafik fungsi eksponen.

Pertumbuhan secara secara eksponensial dapat dituliskan dalam fungsi ( ) = =
, = + 1 dan nilai > , menyatakan laju pertumbuhan, sehingga fungsi eksponen
( ) = dapat donyatakan dalam bentuk

( ) = ( + ) .

Perhatikan contoh berikut dan lengkapi.

Contoh :
Pada awal tahun 2013, Tipou menabung di Bank sebesar Rp. 1.000.000,00. Bank tersebut
memberikan bunga majemuk 10 % pertahun. Tentukan besar uang Tipou setelah akhir tahun
2018.

Jawab :

Untuk mengetahui berapa besar uang Tipou seleah akhir tahun 2018, lengkapilah titik – titik
pada penyelesaian berikut :

Misalkan uang Tipou yang ditabung dinyatakan dengan M0, bunga majemuk Bank dinyatakan
dengan bilangan desimal i , waktu penyimpanan t tahun dan uang Tipou pada akhir tahun ke –

# MATEMATIKA PEMINATAN # 10