Page 10 - KELOMPOK 4 APLIKASI TURUNAN

BAB 3

KECEKUNGAN

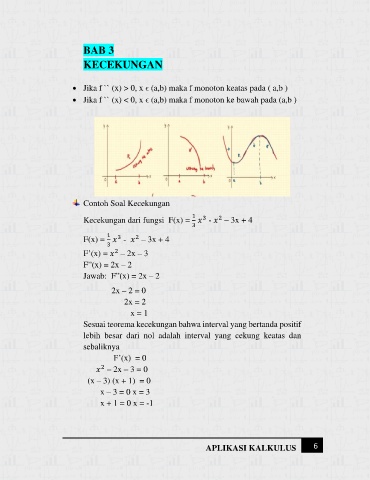
• Jika f `` (x) > 0, x ϵ (a,b) maka f monoton keatas pada ( a,b )

• Jika f `` (x) < 0, x ϵ (a,b) maka f monoton ke bawah pada (a,b )

Contoh Soal Kecekungan

1
3
Kecekungan dari fungsi F(x) = - – 3x + 4
2
3
1
3
2
F(x) = - – 3x + 4
3
F’(x) = – 2x – 3
2
F”(x) = 2x – 2
Jawab: F”(x) = 2x – 2
2x – 2 = 0
2x = 2

x = 1
Sesuai teorema kecekungan bahwa interval yang bertanda positif
lebih besar dari nol adalah interval yang cekung keatas dan
sebaliknya

F’(x) = 0
– 2x – 3 = 0
2
(x – 3) (x + 1) = 0
x – 3 = 0 x = 3
x + 1 = 0 x = -1

APLIKASI KALKULUS 6