Page 153 - Bahan Ajar Metode Statistika
P. 153
Dalil 7.1 Bila X adalh suatu peubah acak binom dengan nilai tengah =
2
dan ragam = , maka bentuk pelimitan bagi sebaran
− , Untuk → ∞, adalah sebaran normal baku
√
Ternyata sebaran normal memberikan hampiran yang sangat baik pada
sebaran binom bila n besar dan p dekat pada ½. Bahkan, bila n kecil dan p
tidak terlalu dekat pada nol atau 1, hampiran itu masih cukup baik.
Untuk menyelidiki hampiran normal bagi sebaran binom, pertama-
tama kita buat histogram bagi b(x; 15, 0.4), kemudian menumpang tindihkan
sebaran normal yang memiliki nilai tengah dan ragam seperti peubah acak
binom X tersebut. Jadi kita menggambar sebuah kurva normal dengan
= = (15)(0.4) = 6
= = (15)(0.4)(0.6) = 3.6
2
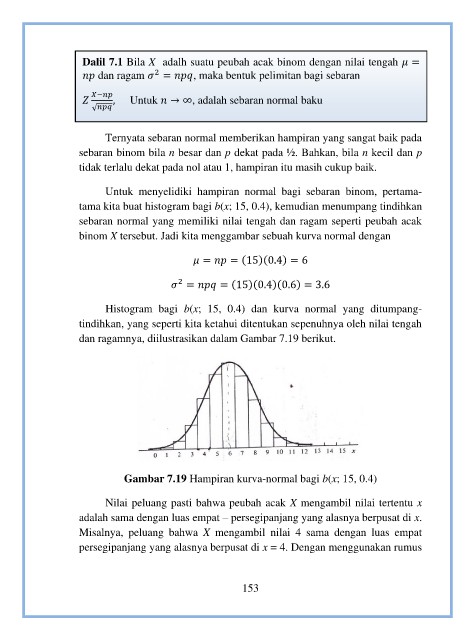
Histogram bagi b(x; 15, 0.4) dan kurva normal yang ditumpang-
tindihkan, yang seperti kita ketahui ditentukan sepenuhnya oleh nilai tengah
dan ragamnya, diilustrasikan dalam Gambar 7.19 berikut.
Gambar 7.19 Hampiran kurva-normal bagi b(x; 15, 0.4)
Nilai peluang pasti bahwa peubah acak X mengambil nilai tertentu x
adalah sama dengan luas empat – persegipanjang yang alasnya berpusat di x.
Misalnya, peluang bahwa X mengambil nilai 4 sama dengan luas empat
persegipanjang yang alasnya berpusat di x = 4. Dengan menggunakan rumus
153