Page 172 - Bahan Ajar Metode Statistika

*)  adalah suatu nilai tengah yang diajukan dalam H
0
0
**) Penggunaan z atau t tergantung ukuran contoh
contoh besar menggunakan z; contoh kecil menggunakan t.

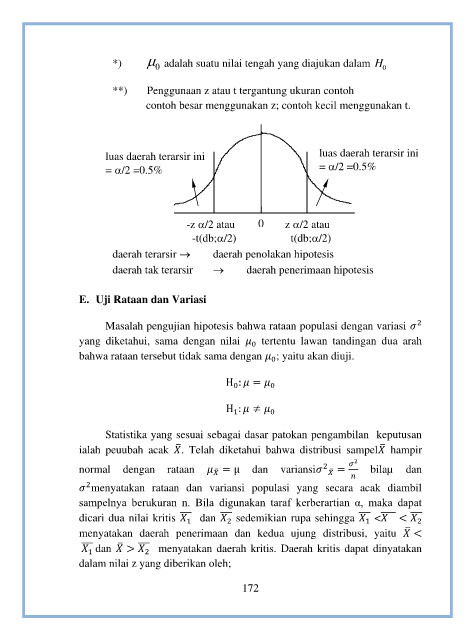
luas daerah terarsir ini luas daerah terarsir ini

= /2 =0.5% = /2 =0.5%

-z /2 atau 0 z /2 atau
-t(db;/2) t(db;/2)
daerah terarsir → daerah penolakan hipotesis
daerah tak terarsir → daerah penerimaan hipotesis

E. Uji Rataan dan Variasi

2
Masalah pengujian hipotesis bahwa rataan populasi dengan variasi
yang diketahui, sama dengan nilai tertentu lawan tandingan dua arah
0
bahwa rataan tersebut tidak sama dengan ; yaitu akan diuji.
0
H : =
0
0
H : ≠
0
1
Statistika yang sesuai sebagai dasar patokan pengambilan keputusan
̅
̅
ialah peuubah acak . Telah diketahui bahwa distribusi sampel hampir
2
normal dengan rataan ̅ = µ dan variansi ̅ = 2 bilaµ dan

menyatakan rataan dan variansi populasi yang secara acak diambil
2
sampelnya berukuran n. Bila digunakan taraf kerberartian α, maka dapat
̅̅̅
̅̅̅ ̅̅̅̅
̅̅̅
̅̅̅
dicari dua nilai kritis 1 dan sedemikian rupa sehingga < <
1
2
2
̅
menyatakan daerah penerimaan dan kedua ujung distribusi, yaitu <
̅̅̅
̅̅̅
̅
dan > 2 menyatakan daerah kritis. Daerah kritis dapat dinyatakan
1
dalam nilai z yang diberikan oleh;
172