Page 270 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
270

● Η συνάρτηση f(χ)=log αχ
είναι συνεχής για
0<α 1 και χ>0

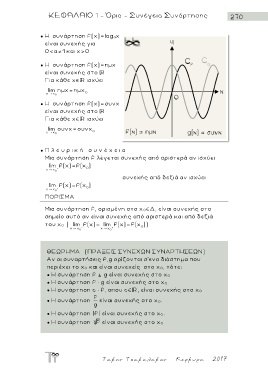
● Η συνάρτηση f(χ)=ημχ
είναι συνεχής στο
Για κάθε χ ισχύει

lim ημx= ημx
x x 0 0

● Η συνάρτηση f(χ)=συνχ
είναι συνεχής στο
Για κάθε χ ισχύει

lim συνx= συνx
x x 0 0

● Π λ ε υ ρ ι κ ή σ υ ν έ χ ε ι α
Μια συνάρτηση f λέγεται συνεχής από αριστερά αν ισχύει
lim f(x) f(x )
x x 0 - 0
συνεχής από δεξιά αν ισχύει
lim f(x) f(x )
x x 0 + 0
ΠΟΡΙΣΜΑ

Μια συνάρτηση f, ορισμένη στο χ 0 Δ, είναι συνεχής στο
σημείο αυτό α ν είναι συνεχής από αριστερά και από δεξιά

του χ 0 ( lim f(x) lim f(x) f(x ))
0
x x 0 - x x 0 +

ΘΕΩΡΗΜΑ (ΠΡΑΞΕΙΣ ΣΥΝΕΧΩΝ ΣΥΝΑΡΤΗΣΕΩΝ)
Αν οι συναρτήσεις f,g ορίζονται σ’ενα διάστημα που
περιέχει το x 0 και είναι συνεχείς στο x 0, τότε:
● Η συνάρτηση f ± g είναι συνεχής στο x 0
● Η συνάρτηση f ∙ g είναι συνεχής στο x 0

● Η συνάρτηση c ∙ f, οπου c , είναι συνεχής στο x 0
f
● Η συνάρτηση είναι συνεχής στο x 0.
g
● Η συνάρτηση |f| είναι συνεχής στο x 0.
● Η συνάρτηση f είναι συνεχής στο x 0
ν

Τακης Τσακαλακος Κερκυρα 2017