Page 152 - olokliroma

152
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

4 4 4 x 3
h(x) dx= (x -4x+3) dx= ( -2x 2 +3x)' dx
2
3 3 3 3

x 3 4 3 3 3 4
= [ -2x 2 +3x ] 4 = -2 4 2 +12-( -2 3 2 +9)=
3 3 3 3 3

Άρα

1 2 3
Ε(Ω) = h(x) dx- h(x) dx+ h(x) dx
0 1 2

4 4 4 4 4 4
= -(- )+ = + + = 4 τ.μ.
3 3 3 3 3 3

Ε ν α λ λ α κ τ ι κ ά

Θεωρούμε τη συνάρτηση

με τύπο
h(x)=f(x)-g(x)=
=x -4x+3
2
● Οι f, g είναι συνεχείς
στο διάστημα [0, 4] σαν
πολυωνυμικές.

● Οι ρίζες της h(x)=0`
x -4x+3=0 είναι
2
ρ 1=1 και ρ 2=3

● ρ 1, ρ 2 [0, 4]

● Οι f, g τέμνουν τον χ'χ
● η f στο (0,0)

3
● η g στο ,0
4

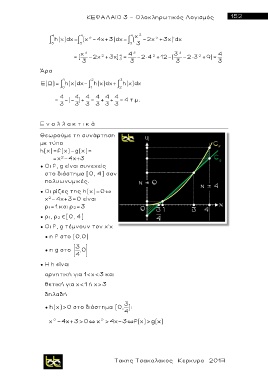
● Η h είναι

αρνητική για 1<χ<3 και

θετική για χ<1 ή χ>3
δηλαδή

3
● h(x)>0 στο διάστημα [0, ] :
4

2
x -4x+3>0` x >4x-3` f(x)>g(x)
2

Τακης Τσακαλακος Κερκυρα 2017