Page 63 - FORMULARIO ALGEBRA

Academia
Formulario de ÁLGEBRA

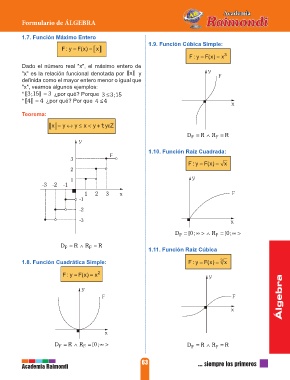
1.7. Función Máximo Entero
1.9. Función Cúbica Simple:
x
Fy: = Fx( ) = 
Fy: = Fx( ) = x 3
Dado el número real "x", el máximo entero de
"x" es la relación funcional denotada por x[ [ ] ] y y
definida como el mayor entero menor o igual que F
"x", veamos algunos ejemplos:
* 3 [[ ; 15 ] ] = 3 ¿por qué? Porque 3 ≤ ; 3 15
* 4[[ ] ] = 4 ¿por qué? Por que 4 ≤ 4 x
Teorema:
x = y ↔ y ≤ x < y +1; yZε
D = R ∧ R = R
F
F
y
1.10. Función Raíz Cuadrada:
F
3
Fy: = Fx( ) = x
2
y
1
-3 -2 -1
1 2 3 x F
-1
-2
-3 x
D F = 0[ ; ∞ > ∧ R F = 0[ ; ∞ >

D = R ∧ R = R 1.11. Función Raíz Cúbica
F
F
1.8. Función Cuadrática Simple: Fy: = Fx( ) = 3 x

Fy: = Fx( ) = x 2 y
Álgebra
y
F F

x

x

D F = R ∧ R F = 0[ ; ∞ > D = R ∧ R = R
F
F
63 ... siempre los primeros
Academia Raimondi