Page 7 - 2020春 中考冲刺讲义第1讲 ---教师

希望多次元数学教研组

【模块二 解答题】
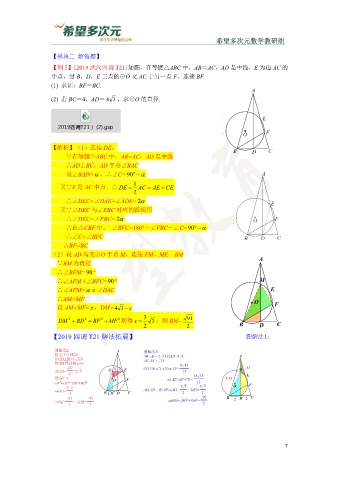
【例 5】[2019 武汉四调 T21]如图，在等腰△ABC 中，AB＝AC，AD 是中线，E 为边 AC 的
中点，过 B，D，E 三点的⊙O 交 AC 于另一点 F，连接 BF
(1) 求证：BF＝BC.

(2) 若 BC＝4，AD＝ 4 3 ，求⊙O 的直径.

2019四调T21） (2).gsp

【解析】（1）连接 DE，
∵在等腰△ABC 中，AB=AC，AD 是中线
∴AD⊥BC，AD 平分∠BAC
设∠BAD= ，∴∠C=90   
1
又∵E 是 AC 中点，∴ DE  AC  AE  CE
2
∴∠DEC=∠DAE+∠ADE= 2
又∵∠DEC 与∠FBC 对应的弧相同
∴∠DEC=∠FBC= 2
∴在△CBF 中， ∠BFC=180°－∠FBC－∠C=90   
∴∠C=∠BFC
∴BF=BC
（2）设 AD 与交⊙O 于点 M，连接 FM，MF, BM
∵BM 为直径
∴∠BFM=90°
∴∠AFM +∠BFC=90 °
∴∠AFM=  ∠DAC
∴AM=MF
设 AM=MF= x ，DM= 4 3  x
3 91
2
2
2
2
DM  BD  BF  MF 解得 x 3 ，则 BM=
2 2
【2019 四调 T21 解法拓展】

7