Page 207 - Maxwell House

SOLUTION OF BASIC EQUATIONS OF ELECTRODYNAMICS 187

Now, we obtain

(−)
0 2 sin(− sin + cos) (4.80)
= + + + = − (2 )
1 3 2 4 0 0
4
2
Here the factor 2 = is the area bounded by the loop and = − sin + cos in
0
0
0
the spherical coordinate system (see Appendix). Therefore,
(−)
0
= − sin (4.81)
0
4
It may seem surprising at first, but this expression is fairly accurate for electrically small loops
2
of any shape including circular when = . In general, more sophisticated analysis can
be done by cutting the loop of any shape into an infinite number of infinitesimal electric dipoles
with uniform current distribution along each of them. Evidently, the simple integral or discrete
sum of the vectorial fields likewise (4.60) gives us the solution while any known amplitude and
phase variations from element to element can be easily incorporated into such analysis.
4.3.3 Loop Antenna as Magnetic Dipole
The electric and magnetic fields radiated by loop can be found putting (4.81) into (4.59). Our
objective here is to demonstrate that the loop antenna is the actual realization of a magnetic
dipole. For the sake of simplicity, we will do it in the far-field area only leaving the near-field
analysis to our reader.
The association between an electric and magnetic dipole can be done following the symmetry
of Maxwell’s equations and the principle of duality (see (4.25)). Making in (4.68) the

substitution required for a magnetic dipole ⟹ , ⟹ −, ⟹ , and 0 ⟹ 1 0
⁄
(recall that ⟺ ) we have
0
0
Electric Dipole Magnetic Dipole Small Loop

∆ ∆ (−) (−)
= 0 sin (−) ⎫⎧ = sin ⎫ ⎧ = ( 0 ) sin
2 ⎪⎪ 2 0 ⎪ ⎪ 2 0

∆ (−) ∆ ⇔
= sin ⎬⎨ = − sin (−) ) sin (−)

2 2 ⎬ ⎨ = −( 0 2
= = = = 0 ⎪⎪ = = = = 0 ⎪ ⎪ = = = = 0
⎭⎩ ⎭ ⎩
(4.82)

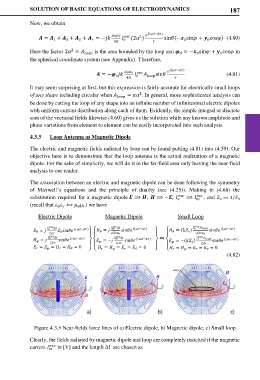
Figure 4.3.5 Near-fields force lines of a) Electric dipole, b) Magnetic dipole, c) Small loop

Clearly, the fields radiated by magnetic dipole and loop are completely matched if the magnetic

current in [V] and the length ∆ are chosen as