Page 870 - Mechatronics with Experiments

856 MECHATRONICS

+
+ Scope
Wind-off speed:
Wind-off roll V1(t)
speed: magnitude is 2.5
10 V1(t)
Scope 1
Wind-off speed:
magnitude is 10.0 w2(t) y(t) F(t)
F_d(t) V2(t) – 1 k
+ 1 s
– Kp tau_m.s+1 r2 + Integrator: Gain:
Desired tension Controller Transfer Fcn1: roll radius speed difference Tension/Displacement
setting: 50 gain Motor and Amp to change in length
k
Tension sensor
Web tension control system model

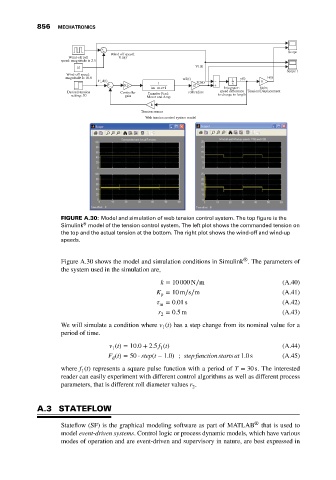
FIGURE A.30: Model and simulation of web tension control system. The top figure is the
®
Simulink model of the tension control system. The left plot shows the commanded tension on
the top and the actual tension at the bottom. The right plot shows the wind-off and wind-up
speeds.

®
Figure A.30 shows the model and simulation conditions in Simulink . The parameters of
the system used in the simulation are,
k = 10 000 N∕m (A.40)
K = 10 m∕s∕m (A.41)
p
= 0.01 s (A.42)
m
r = 0.5 m (A.43)
2
We will simulate a condition where v (t) has a step change from its nominal value for a
1
period of time.
v (t) = 10.0 + 2.5 f (t) (A.44)
1
1
F (t) = 50 ⋅ step(t − 1.0) ; step function starts at 1.0 s (A.45)
d
where f (t) represents a square pulse function with a period of T = 30 s. The interested
1
reader can easily experiment with different control algorithms as well as different process
parameters, that is different roll diameter values r .
2

A.3 STATEFLOW

Stateflow (SF) is the graphical modeling software as part of MATLAB ® that is used to
model event-driven systems. Control logic or process dynamic models, which have various
modes of operation and are event-driven and supervisory in nature, are best expressed in