Page 17 - Contenidos temáticos Ciencias Naturales

P a g e | 12

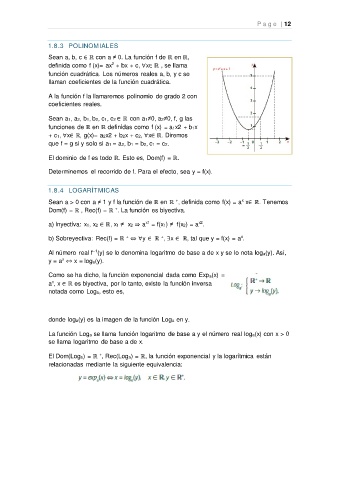
1.8.3 POLINOMIALES

Sean a, b, c ∈ ℝ con a ≠ 0. La función f de ℝ en ℝ,
2
definida como f (x)= ax + bx + c, ∀x∈ ℝ , se llama
función cuadrática. Los números reales a, b, y c se
llaman coeficientes de la función cuadrática.

A la función f la llamaremos polinomio de grado 2 con
coeficientes reales.

Sean a1, a2, b1, b2, c1, c2 ∈ ℝ con a1≠0, a2≠0, f, g las
funciones de ℝ en ℝ definidas como f (x) = a1x2 + b1x
+ c1, ∀x∈ ℝ, g(x)= a2x2 + b2x + c2, ∀x∈ ℝ. Diremos
que f = g si y solo si a1 = a2, b1 = b2, c1 = c2.

El dominio de f es todo ℝ. Esto es, Dom(f) = ℝ.

Determinemos el recorrido de f. Para el efecto, sea y = f(x).

1.8.4 LOGARÍTMICAS
x
+
Sean a > 0 con a ≠ 1 y f la función de ℝ en ℝ , definida como f(x) = a x∈ ℝ. Tenemos
+
Dom(f) = ℝ , Rec(f) = ℝ . La función es biyectiva.
x1
x2
a) Inyectiva: x1, x2 ∈ ℝ, x1 ≠ x2 ⇒ a = f(x1) ≠ f(x2) = a .
+
+
x
b) Sobreyectiva: Rec(f) = ℝ ⇔ ∀y ∈ ℝ , ∃x ∈ ℝ, tal que y = f(x) = a .
–1
Al número real f (y) se lo denomina logaritmo de base a de x y se lo nota loga(y). Así,
x
y = a ⇔ x = loga(y).
Como se ha dicho, la función exponencial dada como Expa(x) =
x
a , x ∈ ℝ es biyectiva, por lo tanto, existe la función inversa
notada como Loga, esto es,

donde loga(y) es la imagen de la función Loga en y.

La función Loga se llama función logaritmo de base a y el número real loga(x) con x > 0
se llama logaritmo de base a de x.

+
El Dom(Loga) = ℝ , Rec(Loga) = ℝ, la función exponencial y la logarítmica están
relacionadas mediante la siguiente equivalencia: