Page 54 - Algebra 2° Sec GM

Funciones lineales

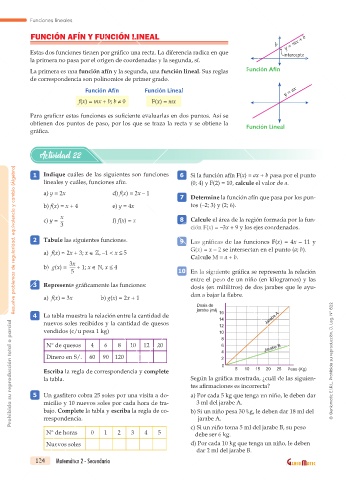
FUNCIÓN AFÍN Y FUNCIÓN LINEAL
b y = mx + b
Estas dos funciones tienen por gráfico una recta. La diferencia radica en que intercepto
la primera no pasa por el origen de coordenadas y la segunda, sí.
La primera es una función afín y la segunda, una función lineal. Sus reglas Función Afín
de correspondencia son polinomios de primer grado.
Función Afín Función Lineal y = ax
f(x) = mx + b; b  0 F(x) = mx

Para graficar estas funciones es suficiente evaluarlas en dos puntos. Así se
obtienen dos puntos de paso, por los que se traza la recta y se obtiene la Función Lineal
gráfica.

Actividad 22

Resuelve problemas de regularidad, equivalencia y cambio (Álgebra)
1 Indique cuáles de las siguientes son funciones 6 Si la función afín F(x) = ax + b pasa por el punto
lineales y cuáles, funciones afín. (0; 4) y F(2) = 10, calcule el valor de a.
a) y = 2x d ) f(x) = 2x – 1
7 Determine la función afín que pasa por los pun-
b) f(x) = x + 4 e) y = 4x tos (–2; 3) y (2; 6).
x
c) y = f ) f(x) = x 8 Calcule el área de la región formada por la fun-
3
ción F(x) = –3x + 9 y los ejes coordenados.
2 Tabule las siguientes funciones. 9 Las gráficas de las funciones F(x) = 4x – 11 y
G(x) = x – 2 se intersectan en el punto (a; b).
a) f(x) = 2x + 3; x  , –1 < x  5
Calcule M = a + b.
3x
b) g(x) = + 1; x  , x  4
5 10 En la siguiente gráfica se representa la relación
entre el peso de un niño (en kilogramos) y las
3 Represente gráficamente las funciones: dosis (en mililitros) de dos jarabes que le ayu-

a) f(x) = 3x b) g(x) = 2x + 1 dan a bajar la fiebre.
Dosis de
jarabe (ml)
4 La tabla muestra la relación entre la cantidad de 16 Jarabe A
14
Prohibida su reproducción total o parcia l
nuevos soles recibidos y la cantidad de quesos 12
vendidos (c/u pesa 1 kg) 10
8
N° de quesos 4 6 8 10 12 20 6 Jarabe B
4
Dinero en S/. 60 90 120 2
 Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
0
Escriba la regla de correspondencia y complete 5 10 15 20 25 Peso (Kg)
la tabla. Según la gráfica mostrada, ¿cuál de las siguien-
tes afirmaciones es incorrecta?
5 Un gasfitero cobra 25 soles por una visita a do- a) Por cada 5 kg que tenga un niño, le deben dar
micilio y 10 nuevos soles por cada hora de tra- 3 ml del jarabe A.
bajo. Complete la tabla y escriba la regla de co- b) Si un niño pesa 30 kg, le deben dar 18 ml del
rrespondencia. jarabe A.
c) Si un niño toma 5 ml del jarabe B, su peso
N° de horas 0 1 2 3 4 5 debe ser 6 kg.

Nuevos soles d) Por cada 10 kg que tenga un niño, le deben
dar 2 ml del jarabe B.
124 Matemática 2 - Secundaria