Page 56 - Geometria 1° Sec GM

Geometría analítica IV

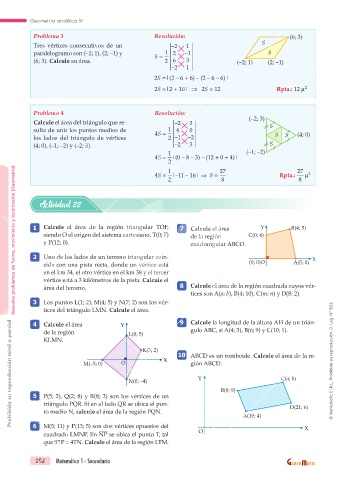
Problema 3 Resolución: (6; 3)
S
–2 1
Tres vértices consecutivos de un
1 2 –1
paralelogramo son (–2; 1), (2; –1) y S = S
(6; 3). Calcule su área. 2 6 3 (–2; 1) (2; –1)
–2 1
2S =|(2 – 6 + 6) – (2 – 6 – 6)|
2S =|2 + 10|  2S = 12 Rpta.: 12 m 2

Problema 4 Resolución:
(–2; 3)
Calcule el área del triángulo que re- S
–2 3
sulta de unir los puntos medios de 4S =
1 4 0
los lados del triángulo de vértices 2 –1 –2 S S (4; 0)
(4; 0), (–1; –2) y (–2; 3). –2 3 S
1 (–1; –2)
4S = |(0 – 8 – 3) – (12 + 0 + 4)|
2
Resuelve problemas de forma, movimiento y localización (Geometría)
1 27 27
4S = |–11 – 16|  S = Rpta.: m 2
2 8 8

Actividad 22

1 Calcule el área de la región triangular TOP, 7 Calcule el área Y B(4; 5)
siendo O el origen del sistema cartesiano, T(0; 7) de la región C(0; 4)
y P(12; 0). cuadrangular ABCO.

2 Uno de los lados de un terreno triangular coin- X
cide con una pista recta, donde un vértice está (0; 0)O A(5; 0)
en el km 34, el otro vértice en el km 38 y el tercer
vértice está a 3 kilómetros de la pista. Calcule el
área del terreno. 8 Calcule el área de la región cuadrada cuyos vér-
tices son A(a; b), B(4; 10), C(m; n) y D(8; 2).
3 Los puntos L(1; 2), M(4; 5) y N(7; 2) son los vér-
tices del triángulo LMN. Calcule el área.

Prohibida su reproducción total o parcia l
4 Calcule el área Y 9 Calcule la longitud de la altura AH de un trián-
de la región L(0; 5) gulo ABC, si A(4; 3), B(6; 9) y C(10; 1).
KLMN.
K(3; 2)
10 ABCD es un romboide. Calcule el área de la re-
X  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
M(–5; 0) O gión ABCD.

N(0; –4) Y C(a; b)
B(8; 9)
5 P(5; 2), Q(2; 8) y R(8; 2) son los vértices de un
triángulo PQR. Si en el lado QR se ubica el pun- D(21; 6)
to medio N, calcule el área de la región PQN.
A(10; 4)
6 M(5; 11) y P(13; 5) son dos vértices opuestos del X
cuadrado LMNP. En NP se ubica el punto T, tal O
que 5TP = 4TN. Calcule el área de la región LTM.

192 Matemática 1 - Secundaria