Page 132 - 16 Fermat

1660. Sin embargo, se publicó de
8 forma anónima. Su autor sola-
mente se identificaba por unas
iniciales que no se correspondían
con las de Fermat. Los seguidores
de Descartes, emulando al maes-
tro, estaban convencidos de que
Aristóteles tenía razón. Fermat,
en su tratado, había decidido de-
A e
mostrar que los cartesianos se
equivocaban.
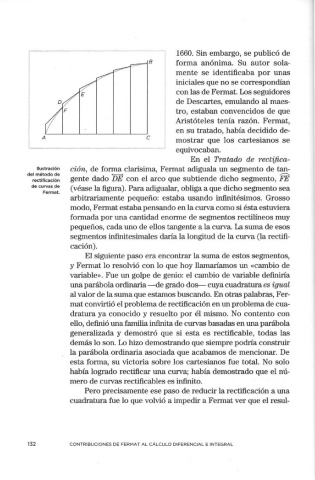
En el Tratado de rectifica-
Ilustración ción, de forma clarísima, Fermat adiguala un segmento de tan-
del método de gente dado DE con el arco que subtiende dicho segmento, FE
rectificación
de curvas de (véase la figura). Para adigualar, obliga a que dicho segmento sea
Fermat.
arbitrariamente pequeño: estaba usando infinitésimos. Grosso
modo, Fermat estaba pensando en la curva como si ésta estuviera
formada por una cantidad enorme de segmentos rectilíneos muy
pequeños, cada uno de ellos tangente a la curva. La suma de esos
segmentos infinitesimales daría la longitud de la curva (la rectifi-
cación).
El siguiente paso era encontrar la suma de estos segmentos,
y Fermat lo resolvió con lo que hoy llamarían10s un «cambio de
variable». Fue un golpe de genio: el cambio de variable definiría
una parábola ordinaria -de grado dos- cuya cuadratura es igual
al valor de la suma que estamos buscando. En otras palabras, Fer-
mat convirtió el problema de rectificación en un problema de cua-
dratura ya conocido y resuelto por él mismo. No contento con
ello, definió una familia infinita de curvas basadas en una parábola
generalizada y demostró que si esta es rectificable, todas las
demás lo son. Lo hizo demostrando que siempre podría construir
la parábola ordinaria asociada que acabamos de mencionar. De
esta forma, su victoria sobre los cartesianos fue total. No solo
había logrado rectificar una curva; había demostrado que el nú-
mero de curvas rectificables es infinito.
Pero precisamente ese paso de reducir la rectificación a una
cuadratura fue lo que volvió a impedir a Fermat ver que el resul-

132 CONTRIBUCIONES DE FERMAT AL CÁLCULO DIFERENCIAL E INTEGRAL