Page 22 - KALKULUS 2 EMY SOHILAIT

E. Fungsi Logaritma Asli

Walaupun kelihatannya sederhana,  dx tidak dapat diselesaikan sebagaimana
x

halnya integral dari fungsi polinom, rasional dan trigonometri yang sudah lazim
kita kenal. Oleh karena itu, dicoba didefinisikan suatu fungsi baru yang

dinamakan fungsi logaritma natural atau fungsi logaritma asli.

Definisi

Fungsi logaritma asli, ditulis sebagai ln , didefinisikan dengan

x 1
ln x   dt, x  0
1 t
Daerah definisinya adalah himpunan bilangan riil positif.

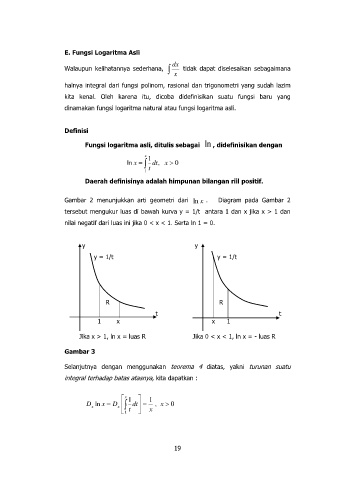
Gambar 2 menunjukkan arti geometri dari . Diagram pada Gambar 2
x
ln
tersebut mengukur luas di bawah kurva y = 1/t antara 1 dan x jika x > 1 dan
nilai negatif dari luas ini jika 0 < x < 1. Serta ln 1 = 0.

y y
y = 1/t y = 1/t

R R

t t
1 x x 1

Jika x > 1, ln x = luas R Jika 0 < x < 1, ln x = - luas R

Gambar 3

Selanjutnya dengan menggunakan teorema 4 diatas, yakni turunan suatu
integral terhadap batas atasnya, kita dapatkan :

 x 1  1
D x ln  D x  dt   , x  0
x
1  t  x

19