Page 75 - KALKULUS 2 EMY SOHILAIT

Jadi sebuah kurva rata dapat dinyatakan dalam sepasang persamaan parameter
x = f(t), y = g(t), a ≤ t ≤ b, kita andaikan fungsi f dan g kontinu pada selang

tersebut. Anggaplah t menyatakan waktu. Apabila t bertambah dari a hinga b,
maka titik (x, y) bergerak sepanjang kurva.

Contoh

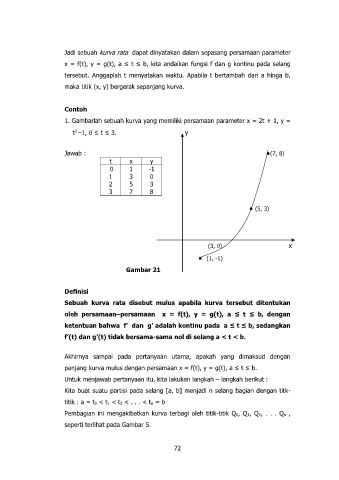
1. Gambarlah sebuah kurva yang memiliki persamaan parameter x = 2t + 1, y =
t –1, 0 ≤ t ≤ 3. y
2

Jawab : ●(7, 8)
t x y
0 1 -1
1 3 0
2 5 3
3 7 8

● (5, 3)

(3, 0) x

● (1, -1)
Gambar 21

Definisi

Sebuah kurva rata disebut mulus apabila kurva tersebut ditentukan
oleh persamaan–persamaan x = f(t), y = g(t), a ≤ t ≤ b, dengan
ketentuan bahwa f’ dan g’ adalah kontinu pada a ≤ t ≤ b, sedangkan

f’(t) dan g’(t) tidak bersama-sama nol di selang a < t < b.

Akhirnya sampai pada pertanyaan utama, apakah yang dimaksud dengan

panjang kurva mulus dengan persamaan x = f(t), y = g(t), a ≤ t ≤ b.
Untuk menjawab pertanyaan itu, kita lakukan langkah – langkah berikut :

Kita buat suatu partisi pada selang [a, b] menjadi n selang bagian dengan titk-
titik : a = t0 < t1 < t2 < . . . < tn = b

Pembagian ini mengakibatkan kurva terbagi oleh titik-titik Q0, Q1, Q2, . . . Qn ,
seperti terlihat pada Gambar 5.

72