Page 27 - II - Geometría 4

Geometría 4° Secundaria

ÁREA DE REGIONES CIRCULARES

REGIONES POLIGONALES

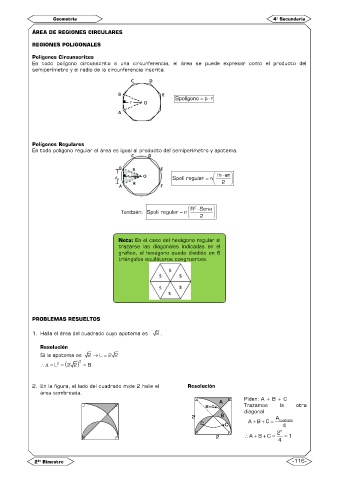
Polígonos Circunscritos
En todo polígono circunscrito a una circunferencia, el área se puede expresar como el producto del
semiperímetro y el radio de la circunferencia inscrita.

Spolígono  p r 

Polígonos Regulares
En todo polígono regular el área es igual al producto del semiperímetro y apotema.

 n an 
Spolí regular   n 
 2 

 R  2 Sen  
También: Spolí regular   n 
 2 

Nota: En el caso del hexágono regular al
trazarse las diagonales indicadas en el
gráfico, el hexágono queda dividido en 6
triángulos equiláteros congruentes.

PROBLEMAS RESUELTOS

1. Halla el área del cuadrado cuyo apotema es 2 .

Resolución
Si la apotema es 2  L  2 2
2
  L  2 2   8
2

2. En la figura, el lado del cuadrado mide 2 halle el Resolución
área sombreada.
Piden: A + B + C
Trazamos la otra
diagonal
A
A B C  cuadrado


4
2 2
 A  B  C  4  1

2 Bimestre -116-
do