Page 70 - u4

P1: OSO/OVY
GO01962-Smith-v1.cls
UAE-Math-Grade-12-Vol-1-SE-718383-ch4
CHAPTER 4 • •
Applications of Differentiation
260 P2: OSO/OVY QC: OSO/OVY T1: OSO October 25, 2018 17:24 4-50
′′
- 0 + Drawing number lines for the factors of f (x), we have
12(x + 2)
-2
- 0 + { > 0, on (−∞, −2) ∪ (−1, ∞)
(x + 1) ′′ Concave up.
-1 f (x)
+ 0 - 0 + < 0, on (−2, −1). Concave down.
f��(x)
-2 -1
From this, we see that there are inflection points at x =−2 and at x =−1. Finally, to
find the x-intercepts, we need to solve f(x) = 0 approximately. Doing this (for
- 0 - 0 +
f�(x) instance, by using Newton’s method or your calculator’s solver), we find that there
-2 - 1
2 are two x-intercepts: x =−1 (exactly) and x ≈−0.160713. Notice that the significant
1
+ 0 - 0 + x-values that we have identified are x =−2,x =−1 and x =− . Computing the
f��(x) 2
-2 -1 corresponding y-values from y = f(x), we get the points (−2, 1), (−1, 0) and
( )
1
− , − 11 . We summarize the first and second derivative information in the
2 16
y number lines in the margin. In Figure 4.65, we include all of these important points
by setting the x-range to be −4 ≤ x ≤ 1 and the y-range to be −2 ≤ y ≤ 8.
8
6
In example 6.2, we examine a function that has local extrema, inflection points
4 and both vertical and horizontal asymptotes.
2
x
-4 -3 -2 -1 1 EXAMPLE 6.2 Drawing a Graph of a Rational Function
-2
2
x − 3
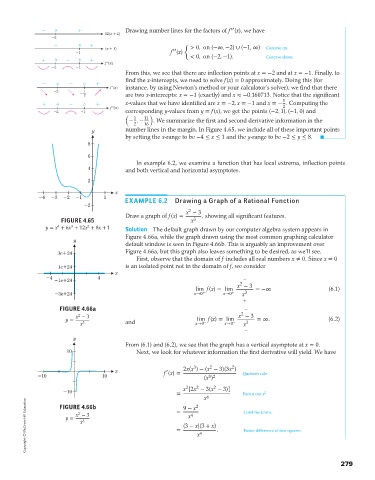
Draw a graph of f(x) = , showing all significant features.
FIGURE 4.65 x 3
3
4
2
y = x + 6x + 12x + 8x + 1 Solution The default graph drawn by our computer algebra system appears in
Figure 4.66a, while the graph drawn using the most common graphing calculator
y
default window is seen in Figure 4.66b. This is arguably an improvement over
3e 24 Figure 4.66a, but this graph also leaves something to be desired, as we’ll see.
+
First, observe that the domain of f includes all real numbers x ≠ 0. Since x = 0
+
1e 24 is an isolated point not in the domain of f, we consider
x
-4 -1e 24 4 −
+
2
lim f(x) = lim x − 3 = −∞ (6.1)
-3e 24 x→0 + x→0 + x 3
+
+
FIGURE 4.66a −
2
2
y = x − 3 lim f(x) = lim x − 3 =∞. (6.2)
x 3 and x→0 − x→0 − x 3
−
y
From (6.1) and (6.2), we see that the graph has a vertical asymptote at x = 0.
10 Next, we look for whatever information the first derivative will yield. We have
3
2
2
′
x f (x) = 2x(x ) − (x − 3)(3x )
-10 10 (x ) Quotient rule.
3 2
2
2
2
x [2x − 3(x − 3)]
-10 = 9 − x 2 x 6 Factor out x .
2
Copyright © McGraw-Hill Education y = x − 3 = (3 − x)(3 + x) . Combine terms.
FIGURE 4.66b
2
4
x
x
3
=
Factor difference of two squares.
4
x
279