Page 15 - HS 8 Afgeleiden

GeoGebra in de derde graad

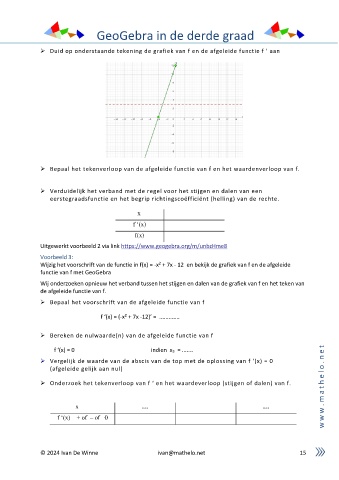
➢ Duid op onderstaande tekening de grafiek van f en de afgeleide functie f ’ aan

➢ Bepaal het tekenverloop van de afgeleide functie van f en het waardenverloop van f.

➢ Verduidelijk het verband met de regel voor het stijgen en dalen van een
eerstegraadsfunctie en het begrip richtingscoëfficiënt (helling) van de rechte.

x
f ‘(x)

f(x)
Uitgewerkt voorbeeld 2 via link https://www.geogebra.org/m/unbzHme8

Voorbeeld 3:
Wijzig het voorschrift van de functie in f(x) = -x + 7x - 12 en bekijk de grafiek van f en de afgeleide
2
functie van f met GeoGebra

Wij onderzoeken opnieuw het verband tussen het stijgen en dalen van de grafiek van f en het teken van
de afgeleide functie van f.

➢ Bepaal het voorschrift van de afgeleide functie van f

f ‘(x) = (-x² + 7x -12)’ = .............

➢ Bereken de nulwaarde(n) van de afgeleide functie van f

t
f ‘(x) = 0 indien x3 = ....... e
n
➢ Vergelijk de waarde van de abscis van de top met de oplossing van f ‘(x) = 0 .
(afgeleide gelijk aan nul) o
l
e
➢ Onderzoek het tekenverloop van f ‘ en het waardeverloop (stijgen of dalen) van f. h
t
a
m
x … … .
w
f ‘(x) + of – of 0 w
w

© 2024 Ivan De Winne ivan@mathelo.net 15