Page 18 - HS 8 Betrouwbaarheidsintervallen

Combinatieleer, kansrekening en verklarende statistiek

Stel dat in 2023 15% van de Belgen dagelijks rookte.
De populatieproportie is dus = 0,15
Bij het uitvoeren van een steekproef zal de steekproefproportie ̂ (notatie p-hoedje) zelden gelijk zijn
aan de populatieproportie = 0,15 (15%) .
Het zal uiteraard bijna nooit gebeuren dat een steekproef als antwoord voor de steekproefproportie
5 % of 80 % als antwoord zal geven. Men zal waarden verwachten die in de buurt van de
populatieproportie van 15 % gelegen zijn.
Om hierop een antwoord te krijgen, onderzoeken wij welke waarde de steekproefproportie ̂ kan
aannemen.
̂
Verschillende steekproeven uit dezelfde populatie geven verschillende steekproefproporties die
allemaal een benadering zijn dan de populatieproportie die men zou vinden indien men alle
Vlamingen deze vraag zou stellen. Men verschijnsel noemt men de steekproefvariabiliteit.
Deze steekproefvariabiliteit kan men onderzoeken door een groot aantal steekproeven (aselect en
representatief) te nemen.
Stel dat men 50 steekproeven neemt met telkens 100 deelnemers.

Van elke steekproef telt men het aantal rokers en de steekproefproporties.
Steekproef 1: 15 rokers, Steekproef 2: 17 rokers, Steekproef 3: 16 rokers , Steekproef 4: 11 rokers…

Men kan deze werkwijze blijven herhalen voor de 50 steekproeven.

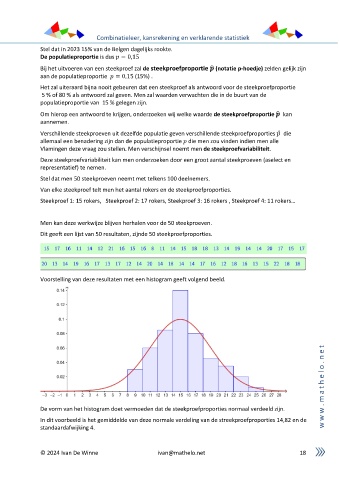
Dit geeft een lijst van 50 resultaten, zijnde 50 steekproefproporties.

Voorstelling van deze resultaten met een histogram geeft volgend beeld.

t
e
n
.
o
l
e
h
t
a
m
.
De vorm van het histogram doet vermoeden dat de steekproefproporties normaal verdeeld zijn. w

In dit voorbeeld is het gemiddelde van deze normale verdeling van de streekproefproporties 14,82 en de w
standaardafwijking 4. w

© 2024 Ivan De Winne ivan@mathelo.net 18