Page 155 - Mathematics 1
P. 155
[ ]6-6-2الرصف ومساحة الرصف Paving and Paving Area
•تسمى عملية ترتيب المضلعات متجاورة بعضها إلى بعض بنمط معين بحيث تغطي كامل المنطقة التي
يراد العمل عليها من دون تداخل فيما بينها ،ومن دون ترك أية فراغات بالـ (الرصف).
•يشترط لإتمام عملية الرصف بشكل صحيح أن تكون قياسات الزوايا الملتقية في الرصف هي ()360
درجة.
•لاتخاذ القرار بشأن صلاحية مضلع منتظم ليكون أساساً للرصف ينبغي أن يكون حاصل قسمة ()360
درجة على قياس زاوية المضلع المنتظم عدداً صحيحا أي أن تكون القسمة من دون با ٍق.
•ُتحدد عدد قطع المضلع المنتظم المستعمل أساساً للرصف بقسمة المساحة المطلوب رصفها على مساحة
الوحدة التي تستعمل للرصف (قطعة السيراميك مثلًا) التي غالبا ما يكون لها قياسات ثابتة.
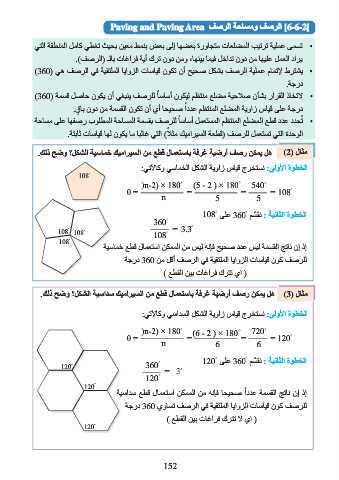
مثال ( (2هل يمكن رصف أرضية غرفة باستعمال قطع من السيراميك خماسية الشكل؟ وضح ذلك.
الخطوة الأولى :نستخرج قياس زاوية الشكل الخماسي وكالآتي:
ْ108
)n-2) × 180° (5 - 2 ) × 180° 540°
θ = n = 5 = 5 = 108°
ْ108ْ 108 الخطوة الثانية :نق ّسم 360°على 108°
ْ108 360°
= 3.3°
108°
إذ إن ناتج القسمة ليس عدد صحيح فإنه ليس من الممكن استعمال قطع خماسية
للرصف كون قياسات الزوايا الملتقية في الرصف أقل من 360درجة
( اي تترك فراغات بين القطع )
مثال ( (3هل يمكن رصف أرضية غرفة باستعمال قطع من السيراميك سداسية الشكل؟ وضح ذلك.
الخطوة الأولى :نستخرج قياس زاوية الشكل السداسي وكالآتي:
)n-2) × 180° = (6 - 2 ×) =180° 720°
θ= n 6 6 = 120°
ْ120 360° الخطوة الثانية :نق ّسم 360°على 120°
ْ120 = 3°
ْ120 120°
إذ إن ناتج القسمة عدداً صحيحا فإنه من الممكن استعمال قطع سداسية
للرصف كون قياسات الزوايا الملتقية في الرصف تساوي 360درجة
( اي لا تترك فراغات بين القطع )
152