Page 84 - 수학(하)

. 2 무리함수의 그래프

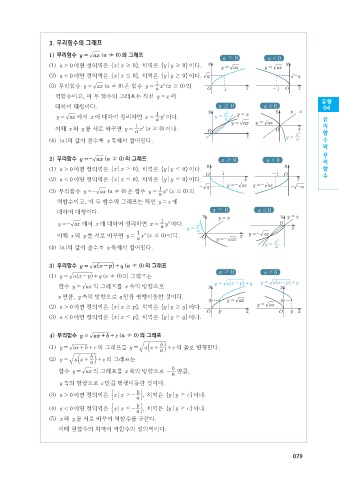
) 1 무리함수 y = ax a ! 0g 의 그래프
]
a $ 0 a < 0
|
1 ]g a > 이면 정의역은 xx $ 0, , 치역은 yy $ 0, 이다. y y = ax y = ax y
|
0
"
"
|
2 ]g a < 이면 정의역은 xx # 0, , 치역은 yy $ 0, 이다. a - a
|
0
"
"
2
3 ]g 무리함수 y = ax a ! 0g 은 함수 y = 1 x x $ 0g 의 O 1 x - 1 O x
]
]
a
x
역함수이고, 이 두 함수의 그래프는 직선 y = 에
유형
대하여 대칭이다. a $ 0 a < 0 04
1 y x 2 y = x y y = x
2
y = ax 에서 x 에 대하여 정리하면 x = a y 이다. y = a 유
1 y = ax y = ax 리
이때 x 와 y 를 서로 바꾸면 y = a x x $ 0g 이다. O O x
2
]
x y = x 2 함
4 ]g a 의 값이 클수록 x 축에서 멀어진다. a 수
와
무
) 2 무리함수 y =- ax a ! 0g 의 그래프 a $ 0 a < 0 리
]
y y
|
|
1 ]g a > 이면 정의역은 xx $ 0, , 치역은 yy # 0, 이다. 함
0
"
"
O 1 - 1 O 수
2 ]g a < 이면 정의역은 xx # 0, , 치역은 yy # 0, 이다. x x
|
|
0
"
"
1 - a y =- ax y =- ax -- a
2
3 ]g 무리함수 y =- ax a ! 0g 은 함수 y = a x x # 0g 의
]
]
x
역함수이고, 이 두 함수의 그래프는 직선 y = 에
대하여 대칭이다. a $ 0 a < 0
y y = x y y = x
1
2
y =- ax 에서 x 에 대하여 정리하면 x = a y 이다. x 2 O x
1 y = a y =- ax
2
이때 x 와 y 를 서로 바꾸면 y = x x # 0g 이다. x
]
a O y =- ax 2
y = x
4 ]g a 의 값이 클수록 x 축에서 멀어진다. a
3) 무리함수 y = a x - h q a ! 0g 의 그래프
p +
]
^
a $ 0 a < 0
1 ]g y = a x - h q a ! 0g 의 그래프는
p + ]
^
p +
y = a x - h q y = a x - h q
p +
^
^
함수 y = ax 의 그래프를 x 축의 방향으로 y y
p 만큼, y 축의 방향으로 q 만큼 평행이동한 것이다.
q y = ax q
|
|
0
2 ]g a > 이면 정의역은 xx $ p, , 치역은 yy $ q, 이다. y = ax
"
"
O p x O p x
0
3 ]g a < 이면 정의역은 xx # p, , 치역은 yy $ q, 이다.
|
|
"
"
b
4) 무리함수 y = ax ++ c a ! 0g 의 그래프
]
b
c
b
1 ]g y = ax + + 의 그래프를 y = a x + l + c 의 꼴로 변형한다.
b
a
b
2 ]g y = a x + l + c 의 그래프는
b
a
b
함수 y = ax 의 그래프를 x 축의 방향으로 - a 만큼,
y 축의 방향으로 c 만큼 평행이동한 것이다.
b
|
0
3 ]g a > 이면 정의역은 xx $- 0 치역은 yy $ c, 이다.
,
|
&
"
a
b
,
|
0
|
4 ]g a < 이면 정의역은 xx #- 0 치역은 yy $ c, 이다.
&
"
a
5 ]g x 와 y 를 서로 바꾸어 역함수를 구한다.
이때 원함수의 치역이 역함수의 정의역이다.
079