Page 167 - 수학(상)

풀이 42쪽

k
기출 맛보기 315 직선 y = x 2 + 를 x 축의 방향으로 2 만큼,
-
y 축의 방향으로 3 만큼 평행이동한 직선이
y
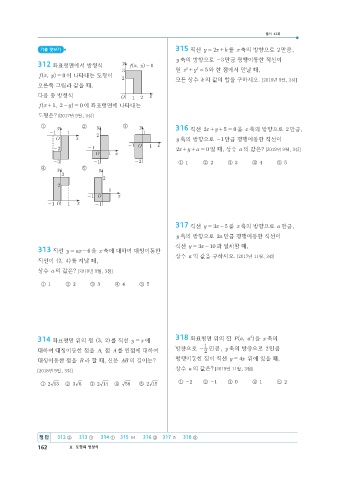
312 좌표평면에서 방정식 f^ , xy = 0 2 2
h
5
3 원 x + y = 와 한 점에서 만날 때,
0
h
f^ , xy = 이 나타내는 도형이
2 모든 상수 k 의 값의 합을 구하시오. [2018년 9월, 3점]
오른쪽 그림과 같을 때,
다음 중 방정식 O 1 2 x
f x + , 12 - h 0
y = 이 좌표평면에 나타내는
^
도형은? [2017년 9월, 3점]
① y ② y ③ y 316 직선 x2 ++ 5 = 을 x 축의 방향으로 2 만큼,
y
0
- 1 1 2 1
O x y 축의 방향으로 1만큼 평행이동한 직선이
-
- 1 O 1 x
- 2 - 1 x 2 ++ a = 일 때, 상수 a 의 값은? [2019년 9월, 3점]
0
y
O 1 x
- 3 - 1 - 2 ① 1 ② 2 ③ 3 ④ 4 ⑤ 5
④ y ⑤ y
3
2
2
1
- 1 O x
- 1 O 1 x - 1
5
317 직선 y = x 3 - 를 x 축의 방향으로 a 만큼,
2
y 축의 방향으로 a 만큼 평행이동한 직선이
직선 y = x 3 - 10 과 일치할 때,
313 직선 y = ax - 을 x 축에 대하여 대칭이동한
6
상수 a 의 값을 구하시오. [2017년 11월, 3점]
직선이 ,24h 를 지날 때,
^
상수 a 의 값은? [2018년 9월, 3점]
① 1 ② 2 ③ 3 ④ 4 ⑤ 5

2
,
^
x
314 좌표평면 위의 점 ,32h 를 직선 y = 에 318 좌표평면 위의 점 P aa h 을 x 축의
^
방향으로 - 1 만큼, y 축의 방향으로 2 만큼
대하여 대칭이동한 점을 ,A 점 A 를 원점에 대하여 2
평행이동한 점이 직선 y = x 4 위에 있을 때,
대칭이동한 점을 B 라 할 때, 선분 AB 의 길이는?
상수 a 의 값은? [2019년 11월, 3점]
[2018년 9월, 3점]
-
-
① 213 ② 36 ③ 214 ④ 58 ⑤ 215 ① 2 ② 1 ③ 0 ④ 1 ⑤ 2

정답 312 ② 313 ① 314 ① 315 14 316 ② 317 5 318 ⑤
162 Ⅲ . 도형의 방정식