Page 30 - E-Book Kalkulus Integral
P. 30
Jumlahan Riemann merupakan suatu pendekatan untuk menghitung luas suatu
daerah dengan cara membaginya menjadi persegipanjang-persegipanjang kecil,
menghitung luas persegipanjang tersebut dan menjumlahkannya. Proses dilakukan
dengan cara membagi interval menjadi beberapa subinterval dan pada setiap subinterval
tersebut dipilih salah satu titik untuk dihitung nilai fungsinya sebagai titik tinggi.
Selanjutnya dengan membuat asumsi setiap luasan kecil berbentuk persegipanjang
maka luas persegipanjang kecil diperoleh dengan cara nilai fungsi dikalikan dengan
lebar subinterval.
2
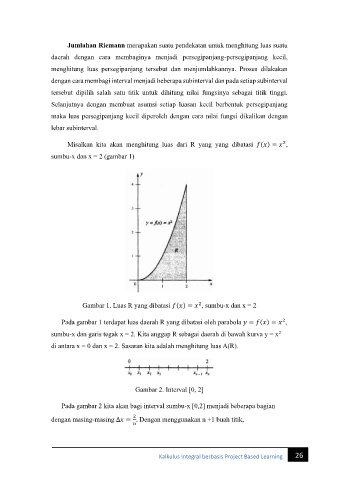
Misalkan kita akan menghitung luas dari R yang yang dibatasi ( ) = ,
sumbu-x dan x = 2 (gambar 1)
2
Gambar 1. Luas R yang dibatasi ( ) = , sumbu-x dan x = 2
Pada gambar 1 terdapat luas daerah R yang dibatasi oleh parabola = ( ) = ,
2
2
sumbu-x dan garis tegak x = 2. Kita anggap R sebagai daerah di bawah kurva y = x
di antara x = 0 dan x = 2. Sasaran kita adalah menghitung luas A(R).
Gambar 2. Interval [0, 2]
Pada gambar 2 kita akan bagi interval sumbu-x [0,2] menjadi beberapa bagian
2
dengan masing-masing ∆ = . Dengan menggunakan n +1 buah titik,
Kalkulus Integral berbasis Project Based Learning 26