Page 32 - E-Book Kalkulus Integral

2 2 2 8
2
2
( )∆ = ∆ = ( ) . = ( 3 )

Jadi
8 8 8 8
2
2
2
2
( ) = [ (0 ) + (1 ) + (2 ) + ⋯ + ( − 1) ]

3 3 3 3
8
2
2
2
= [1 + 2 + ⋯ + ( − 1) ]
3
8 ( −1) (2 −1)
= [ ], (dengan mengganti − 1 menjadi n maka)
3 6
2
3
8 2 −3 +
= [ ]
6 3
4 3 1
= [2 − + ]
3 2
8 4 4
= − +
3 3 2
Kita simpulkan bahwa

8 4 4 8
( ) = lim ( ) = lim ( − + ) =

→∞ →∞ 3 3 2 3
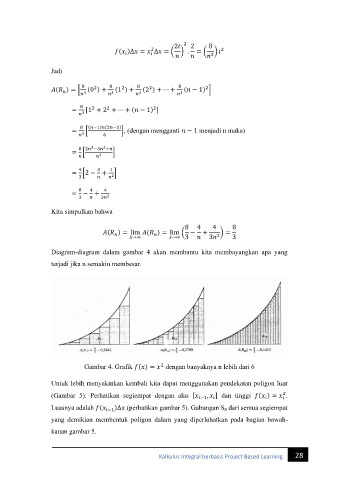
Diagram-diagram dalam gambar 4 akan membantu kita membayangkan apa yang

terjadi jika n semakin membesar.

2
Gambar 4. Grafik ( ) = dengan banyaknya n lebih dari 6
Untuk lebih menyakinkan kembali kita dapat menggunakan pendekatan poligon luar

2
(Gambar 5). Perhatikan segiempat dengan alas [ −1 , ] dan tinggi ( ) = .

Luasnya adalah ( =1 )∆ (perhatikan gambar 5). Gabungan Sn dari semua segiempat
yang demikian membentuk poligon dalam yang diperluhatkan pada bagian bawah-
kanan gambar 5.

Kalkulus Integral berbasis Project Based Learning 28