Page 40 - E-Book Kalkulus Integral

4. Teorema Integral Tentu

a. Teorema Dasar Kalkulus Pertama

Teorema

jika fungsi f kontinu pada interval tertutup [a,b] , maka ( ) = ∫ ( )

kontinu pada [a,b] dan diferensiabel pada (a,b) dan derivatifnya dinyatakan
oleh:

′( ) = ∫ ( ) = ( )

Untuk dapat memahami penggunaan dari konsep teorema integral ini, coba

perhatikan contoh di bawah ini:

Contoh

2

1
Hitunglah [∫ ( + ) ]

1
3
3
Penyelesaian

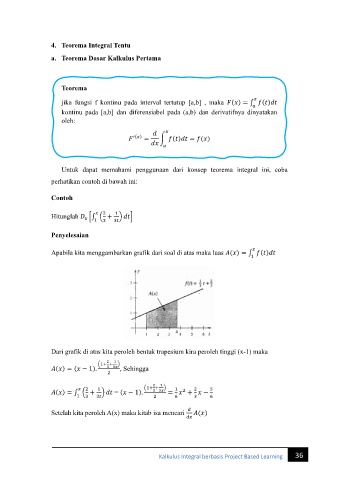
Apabila kita menggambarkan grafik dari soal di atas maka luas ( ) = ∫ ( )
1

Dari grafik di atas kita peroleh bentuk trapesium kira peroleh tinggi (x-1) maka

2 1
(1+ + )
( ) = ( − 1). 3 3 , Sehingga
2
2 1
2 1 (1+ + ) 1 2 5
2
( ) = ∫ ( + ) = ( − 1). 3 3 = + −
1 3 3 2 6 3 6
Setelah kita peroleh A(x) maka kitab isa mencari ( )

Kalkulus Integral berbasis Project Based Learning 36