Page 26 - Modul Aljabar
P. 26
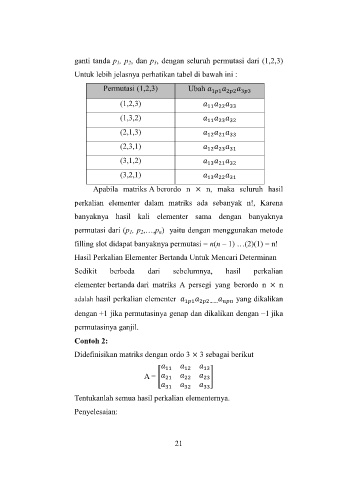
ganti tanda p 1, p 2, dan p 3, dengan seluruh permutasi dari (1,2,3)
Untuk lebih jelasnya perhatikan tabel di bawah ini :
Permutasi (1,2,3) Ubah 1 1 2 2 3 3
(1,2,3)
11 22 33
(1,3,2)
11 23 32
(2,1,3)
12 21 33
(2,3,1)
12 23 31
(3,1,2)
13 21 32
(3,2,1)
13 22 31
Apabila matriks A berordo n × n, maka seluruh hasil
perkalian elementer dalam matriks ada sebanyak n!, Karena
banyaknya hasil kali elementer sama dengan banyaknya
permutasi dari (p 1, p 2,…,p n) yaitu dengan menggunakan metode
filling slot didapat banyaknya permutasi = n(n – 1) …(2)(1) = n!
Hasil Perkalian Elementer Bertanda Untuk Mencari Determinan
Sedikit berbeda dari sebelumnya, hasil perkalian
elementer bertanda dari matriks A persegi yang berordo n × n
adalah hasil perkalian elementer 1 1 2 2…… yang dikalikan
dengan +1 jika permutasinya genap dan dikalikan dengan −1 jika
permutasinya ganjil.
Contoh 2:
Didefinisikan matriks dengan ordo 3 × 3 sebagai berikut
11 12 13
A = [ 21 22 23]
31 32 33
Tentukanlah semua hasil perkalian elementernya.
Penyelesaian:
21