Page 762 - Microeconomics, Fourth Edition

BMappAMathematicalAppendix.qxd 8/17/10 1:10 AM Page 736

736 MATHEMATICAL APPENDIX

y = 4x
B
16

y
A dy
8 dx

4

0 2 4
x x
(a) (b)

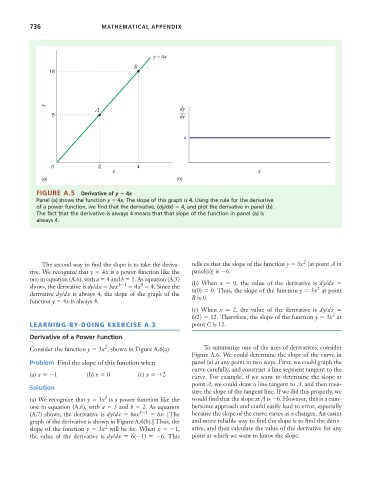
FIGURE A.5 Derivative of y 4x
Panel (a) shows the function y 4x. The slope of this graph is 4. Using the rule for the derivative
of a power function, we find that the derivative, (dy/dx) 4, and plot the derivative in panel (b).
The fact that the derivative is always 4 means that that slope of the function in panel (a) is
always 4.

2
The second way to find the slope is to take the deriva- tells us that the slope of the function y 3x [at point A in
tive. We recognize that y 4x is a power function like the panel(a)] is 6.
one in equation (A.6), with a 4 and b 1. As equation (A.5)
0
shows, the derivative is dy/dx bax b 1 4x 4. Since the (b) When x 0, the value of the derivative is dy/dx
2
derivative dy/dx is always 4, the slope of the graph of the 6(0) 0. Thus, the slope of the function y 3x at point
function y 4x is always 4. B is 0.
(c) When x 2, the value of the derivative is dy/dx
2
6(2) 12. Therefore, the slope of the function y 3x at
LEARNING-BY-DOING EXERCISE A.3 point C is 12.
Derivative of a Power Function
2
Consider the function y 3x , shown in Figure A.6(a). To summarize one of the uses of derivatives, consider
Figure A.6. We could determine the slope of the curve in
Problem Find the slope of this function when panel (a) at any point in two ways. First, we could graph the
curve carefully, and construct a line segment tangent to the
(a) x 1 (b) x 0 (c) x 2 curve. For example, if we want to determine the slope at
point A, we could draw a line tangent to A, and then mea-
Solution
sure the slope of the tangent line. If we did this properly, we
2
(a) We recognize that y 3x is a power function like the would find that the slope at A is 6. However, this is a cum-
one in equation (A.6), with a 3 and b 2. As equation bersome approach and could easily lead to error, especially
(A.7) shows, the derivative is dy/dx bax b 1 6x. [The because the slope of the curve varies as x changes. An easier
graph of the derivative is shown in Figure A.6(b).] Thus, the and more reliable way to find the slope is to find the deriv-
2
slope of the function y 3x will be 6x. When x 1, ative, and then calculate the value of the derivative for any
the value of the derivative is dy/dx 6( 1) 6. This point at which we want to know the slope.