Page 763 - Microeconomics, Fourth Edition

BMappAMathematicalAppendix.qxd 8/17/10 1:10 AM Page 737

A.4 HOW TO FIND A DERIVATIVE 737

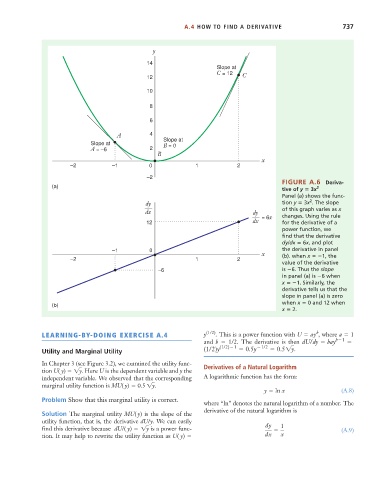
y
14
Slope at
C = 12 C
12

10

8
6

A 4
Slope at
Slope at B = 0
A = –6 2
B
x
–2 –1 0 1 2
–2
FIGURE A.6 Deriva-
(a) 2
tive of y 3x
Panel (a) shows the func-
2
dy tion y 3x . The slope
dx dy of this graph varies as x
dx = 6x changes. Using the rule
12 for the derivative of a
power function, we
find that the derivative
dy/dx 6x, and plot
–1 0 the derivative in panel
x
–2 1 2 (b). when x 1, the
value of the derivative
–6 is 6. Thus the slope
in panel (a) is 6 when
x 1. Similarly, the
derivative tells us that the
slope in panel (a) is zero
when x 0 and 12 when
(b)
x 2.

b
LEARNING-BY-DOING EXERCISE A.4 y (1/2) . This is a power function with U ay , where a 1
and b 1/2. The derivative is then dU/dy bay b 1
Utility and Marginal Utility (1/2)y (1/2) 1 0.5y 1/2 0.51y .

In Chapter 3 (see Figure 3.2), we examined the utility func- Derivatives of a Natural Logarithm
tion U( y) 1y . Here U is the dependent variable and y the
independent variable. We observed that the corresponding A logarithmic function has the form:
marginal utility function is MU( y) 0.5 1y .
y ln x (A.8)
Problem Show that this marginal utility is correct.
where “ln” denotes the natural logarithm of a number. The
derivative of the natural logarithm is
Solution The marginal utility MU( y) is the slope of the
utility function, that is, the derivative dU/y. We can easily
find this derivative because dU/( y) 1y is a power func- dy 1 (A.9)
tion. It may help to rewrite the utility function as U( y) dx x