Page 185 - Fiber Optic Communications Fund

166 Fiber Optic Communications

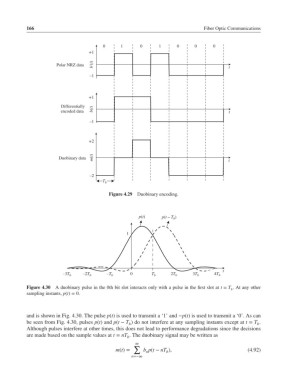
0 1 0 1 0 0 0
+1
Polar NRZ data b'(t) t

–1

+1
Differentially
encoded data b(t) t

–1

+2

Duobinary data m(t) t

–2
T b
Figure 4.29 Duobinary encoding.

p(t) p(t ‒ T b )

1

t
–3T b –2T b –T b 0 T b 2T b 3T b 4T b

Figure 4.30 A duobinary pulse in the 0th bit slot interacts only with a pulse in the first slot at t = T . At any other
b
sampling instants, p(t)= 0.

and is shown in Fig. 4.30. The pulse p(t) is used to transmit a ‘1’ and −p(t) is used to transmit a ‘0’. As can
be seen from Fig. 4.30, pulses p(t) and p(t − T ) do not interfere at any sampling instants except at t = T .
b b
Although pulses interfere at other times, this does not lead to performance degradations since the decisions
are made based on the sample values at t = nT . The duobinary signal may be written as
b
∞
∑
m(t)= b p(t − nT ), (4.92)
b
n
n=−∞