Page 70 - _Turunan Fungsi Aljabar_

59

Contoh soal 17

Sebuah partikel diamati pada interval waktu (dalam menit) tertentu
berbentuk kurva ( ) = − 9 + 24 − 16 pada 0 ≤ ≤ 6. Tentukan nilai
2
3
optimal pergerakan partikel tersebut.
Alternatif Penyelesaian:
′
Daerah asal fungsi adalah { |0 ≤ ≤ 6} Titik stasioner ( ) = 0
3
2
( ) = − 9 + 24 − 16
Sehingga
′
2
′′
( ) = 3( − 6 + 8) = 0 dan ( ) = 6 − 18
( ) = 3( − 2)( − 4) = 0
′
= 2 → (2) = 4 dan = 4 → (4) = 0
Karena daerah asal { |0 ≤ ≤ 6} dan absis = 2, = 4 ada dua
daerah asal sehingga:
= 0 → (0) = −16 dan = 6 → (6) = 20.
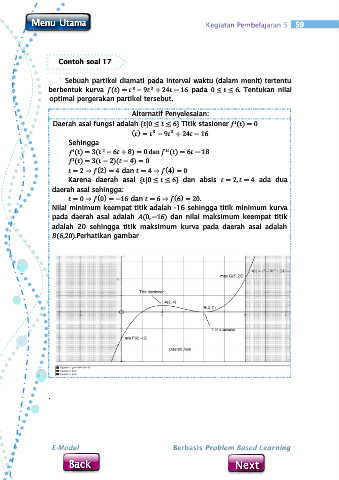
Nilai minimum keempat titik adalah -16 sehingga titik minimum kurva
pada daerah asal adalah (0, −16) dan nilai maksimum keempat titik
adalah 20 sehingga titik maksimum kurva pada daerah asal adalah
(6,20).Perhatikan gambar

.