Page 234 - FUNDAMENTALS OF COMPUTER

234 Fundamentals of Computers NPP

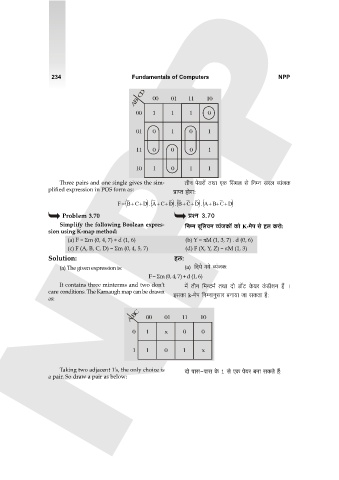
A B C D 00 01 11 10

00 1 1 1 0

01 0 1 0 1

11 0 0 0 1

10 1 0 1 1

Three pairs and one single gives the sim- VrZ no`am| VWm EH$ qgJb go {ZåZ gab ì`§OH$
plified expression in POS form as: àmßV hmoJm:

F = (B+ C+ D ) (A. + C+ D ) (B. + C+ D ) (A. + B+ C+ ) D
Problem 3.70 NPP àíZ 3.70
Simplify the following Boolean expres- {ZåZ ~y{b`Z ì`§OH$m| H$mo K-_on go hb H$amo:
sion using K-map method:
(a) F = Σm (0, 4, 7) + d (1, 6) (b) Y = πM (1, 3, 7) . d (0, 6)
(c) F (A, B, C, D) = Σm (0, 4, 5, 7) (d) F (X, Y, Z) = πM (1, 3)
Solution: hc:
(a) The given expression is: (a) {X`o J`o ì`§OH$:
F = Σm (0, 4, 7) + d (1, 6)
It contains three minterms and two don’t _| VrZ {_ÝQ>_© VWm Xmo S>m|Q> Ho$`a H§$S>reZ h¢ Ÿ&
care conditions. The Karnaugh map can be drawn BgH$m k-_on {ZåZmZwgma ~Zm`m Om gH$Vm h¡:
as:

A B C 00 01 11 10

0 1 x 0 0

1 1 0 1 x

Taking two adjacent 1’s, the only choice is Xmo nmg-nmg Ho$ 1 go EH$ no`a ~Zm gH$Vo h¢:
a pair. So draw a pair as below: