Page 235 - FUNDAMENTALS OF COMPUTER

NPP

NPP Number System, Boolean Algebra and Logic Circuits 235

A B C 00 01 11 10

0 1 x 0 0

1 1 0 1 x

There is only one uncovered ‘1’ . The adja- A~ Ho$db EH$ 1 ~Mm h¡ Ÿ& BgHo$ nmg Ho$ EH$ S>m|Q>
cent don’t care can be used to draw a pair- (do Ho$`a H§$S>reZ H$mo boH$a EH$ no`a Am¡a ~Zm gH$Vo h¢
not make a single) (qgJb Z ~ZmE):
A B C 00 01 11 10

0 1 x 0 0

1 1 0 1 x

We have covered all the 1’s. Therefore con- My±{H$ gmao 1 H$da hmo JE h¢, Bg{bE ~mH$s ~Mo hþE
sider the uncovered ‘X’ as zero. The simplified S>m|Q> Ho$`a H$mo eyÝ` _mZ boVo h¢ Ÿ& Xmo no`am| Ho$ {bE gab
expression for two pairs can be written as:

F = B . C + B . A ì`§OH$ Bg àH$ma go {bI gH$Vo h¢: F = B . C + B . A
Note: Stop making groups as soon as you ZmoQ>- O¡go hr gmao 1 H$da hmo OmE d¡go hr g_yh
cover all the 1’s. In this problem if you make ~ZmZm ~§X H$a X|Ÿ& `{X S>m|Q> Ho$`a H$mo boH$a A{YH$ g_yh
one more pair, that will produce unnecessary
term. ~ZmVo h¢ Vmo do AZmdí`H$ hm|Jo Am¡a Cggo ì`§OH$ Wmo‹S>m ~‹S>m
hmo OmEJmŸ& `h JcV hmoJmŸ&
(b) Y = πM(1, 3, 7) . d (0, 6) (b) Y = πM(1, 3, 7) . d (0, 6)
The above expression contains three Cnamoº$ ì`§OH$ _| VrZ _oŠñQ>_© VWm Xmo S>m|Q> Ho$`a
maxterms and two don’t care conditions. The
K-map and the groups can be drawn as: h¢& BgHo$ J«wn Bg àH$ma ~ZmE Om gH$Vo h¢:
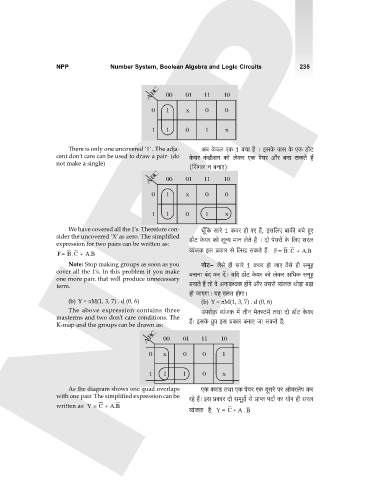
A B C 00 01 11 10

0 x 0 0 1

1 1 1 0 x

As the diagram shows one quad overlaps EH$ ŠdmS> VWm EH$ no`a EH$ Xygao na Amodabon H$a
with one pair. The simplified expression can be aho h¢& Bg àH$ma Xmo g_yhm| go àmßV nXm| H$m `moJ hr gab
written as: Y = C + B . A
ì`§OH$ h¡: Y = C + A . B