Page 29 - FORMULARIO TRIGONOMETRIA - RAIMONDI
P. 29
Academia
Formulario de TRIGONOMETRÍA
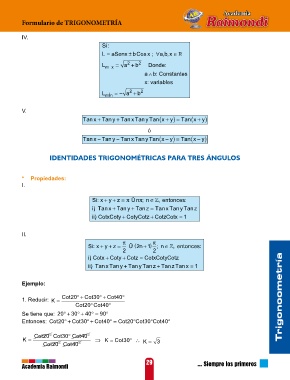
IV.
Si :
L = aSenx bCos;± x ab x,,∀ ∈
2
L m� x = a + b 2 Donde :
ab∧ : Constantes
x: variables
2
L mÌn =− a + b 2
V.
(
Tan x + Tan y + TanTan Tanx y ( x + y) = Tan x + y)
ó
(
Tan x − Tan y − TanTan Tanx y ( x − y) = Tan x y− )
IDENTIDADES TRIGONOMÉTRICAS PARA TRES ÁNGULOS
* Propiedades:
I.
Si: x ++ z = π Û nπ; n ∈ , entonces:
y
i)Tan x + Tan y + Tan z = TanTannTany z
x
) ii CotxCoty CotyCotz CotzCotx+
+ = 1
II.
π π
y
Si: x ++ z = Û (2 n + ) 1 ; n ∈ , entonces:
2 2
iCotxCotyCot+ + z z = CotxCotyCotz
)
z
y
ii )Tan Tan y + Tan Tan z + Tan Tan x = 1
x
Ejemplo:
Cot20 °+ Cot30 °+ Cot40 ° Trigonoometría
1. Reducir: K =
Cot20 ° Cot40 °
Se tiene que: 20°+ 30°+ 40°= 90°
Entonces: Cot20°+ Cot30°+ Cot40°= Cot20° Cot30° Cot40°
Cot20 ° Cot30 ° Cot40 °
K = ⇒ K = Cot30 ° ∴ K = 3
Cot20 ° Cot40 °
29 ... Siempre los primeros
Academia Raimondi