Page 57 - E-MODUL- Aplikasi Turunan dengan Pendekatan RME Berbasis Pemecahan Masalah Polya
P. 57
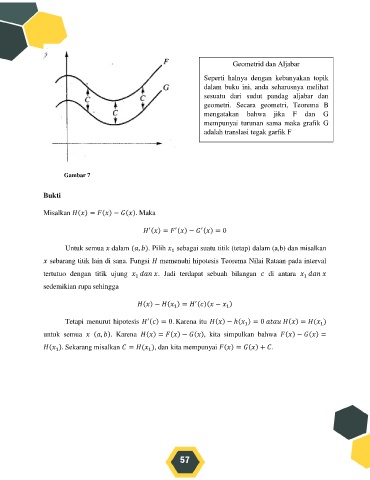
Geometrid dan Aljabar
Seperti halnya dengan kebanyakan topik
dalam buku ini, anda seharusnya melihat
sesuatu dari sudut pandag aljabar dan
geometri. Secara geometri, Teorema B
mengatakan bahwa jika F dan G
mempunyai turunan sama maka grafik G
adalah translasi tegak garfik F
Gambar 7
Bukti
Misalkan ( ) = ( ) − ( ). Maka
′
′
′
( ) = ( ) − ( ) = 0
Untuk semua dalam ( , ). Pilih sebagai suatu titik (tetap) dalam (a,b) dan misalkan
1
sebarang titik lain di sana. Fungsi memenuhi hipotesis Teorema Nilai Rataan pada interval
tertutuo dengan titik ujung . Jadi terdapat sebuah bilangan di antara
1
1
sedemikian rupa sehingga
′
( ) − ( ) = ( )( − )
1
1
Tetapi menurut hipotesis ( ) = 0. Karena itu ( ) − ℎ( ) = 0 ( ) = ( )
′
1
1
untuk semua ( , ). Karena ( ) = ( ) − ( ), kita simpulkan bahwa ( ) − ( ) =
( ). Sekarang misalkan = ( ), dan kita mempunyai ( ) = ( ) + .
1
1
57