Page 32 - Modul Matematika Peminatan Kelas X KD 3.2 (Vektor)

Modul Matematika Peminatan Kelas X KD 3.2

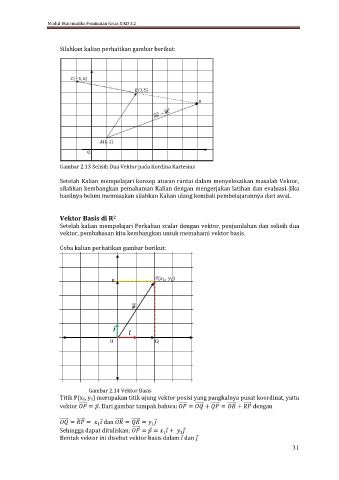
Silahkan kalian perhatikan gambar berikut:

Gambar 2.13 Selisih Dua Vektor pada Kordina Kartesius

Setelah Kalian mempelajari konsep aturan rantai dalam menyelesaikan masalah Vektor,
silahkan kembangkan pemahaman Kalian dengan mengerjakan latihan dan evaluasi. Jika
hasilnya belum memuaskan silahkan Kalian ulang kembali pembelajarannya dari awal.

Vektor Basis di R
2
Setelah kalian mempelajari Perkalian scalar dengan vektor, penjumlahan dan selisih dua
vektor, pembahasan kita kembangkan untuk memahami vektor basis.

Coba kalian perhatikan gambar berikut:

Gambar 2.14 Vektor Basis
Titik P(x1, y1) merupakan titik ujung vektor posisi yang pangkalnya pusat koordinat, yaitu
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
vektor = . Dari gambar tampak bahwa: = + = + dengan

⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ 1 ⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ 1
= = dan = =
⃗⃗⃗⃗⃗
Sehingga dapat dituliskan: = = +
1
1
Bentuk vektor ini disebut vektor basis dalam dan
31