Page 216 - analysinew

216
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΑΠΡΟΣΔΙΟΡΙΣΤΕΣ ΜΟΡΦΕΣ

πρόσθεση (+ )+(- ) ή (- )+(+ )

αφαίρεση (+ )-(+ ) ή (- )-(- )

πολλαπλασιασμός 0 (+ ) ή (+ ) 0 ή 0 (- ) ή (- ) 0

διαίρεση 0 ή ή ή ή
0

● Π ρ ό τ α σ η

αν f(x) g(x) ή f(x)< g(x) για κάθε χ x 0, τότε
lim f(x) x lim g(x)

x
x
x
0
0
● αν lim f(x) + τότε lim g(x) +

x
x
x
x
0
0
● αν lim g(x) - τότε lim f(x) -
x x 0 x x 0
ΑΠΟΔΕΙΞΗ

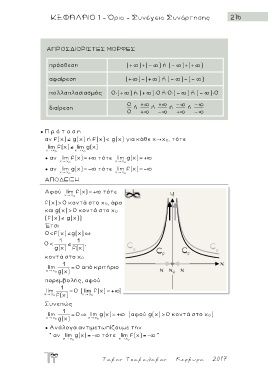
Αφού lim f(x) + τότε
x x 0
f(x)>0 κοντά στο χ 0, άρα

και g(x)>0 κοντά στο χ 0

(f(x) g(x))
Έτσι

0<f(x) g(x)`
1
1

0 g(x) f(x) ,

κοντά στο χ 0
1
lim 0 α π ό κριτήριο
x x 0 g(x)

παρεμβολής, αφού
1
lim 0 ( lim f(x) )
x x 0 f(x) x x 0

Συνεπώς
1
lim 0~ lim g(x) + (αφού g(x)>0 κοντά στο χ 0)
x x 0 g(x) x x 0
● Ανάλογα αντιμετωπίζουμε την

" αν lim g(x) - τότε lim f(x) - "
x x 0 x x 0

Τακης Τσακαλακος Κερκυρα 2017