Page 277 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
277

2. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ (ΠΑΡΑΜΕΤΡΟΣ)
α(x+1)
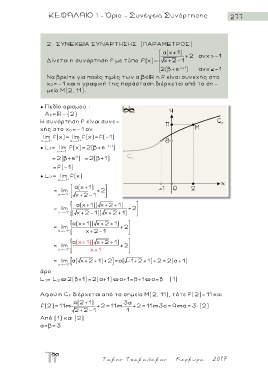
Δίνεται η συνάρτηση f με τύπο f(x)= x+2-1 +2 αν x>-1

2(β+e x + 1 ) αν x - 1
Να βρείτε για ποιές τιμές των α,β η f είναι συνεχής στο
χ 0=-1 και η γραφική της παράσταση διέρχεται από το ση -
μείο Μ(2, 11).

● Πεδίο ορισμού :
Α f= -{2}

Η συνάρτηση f είναι συνε-
χής στο χ 0=-1 αν
lim f(x)= lim f(x)=f(-1)
x -1 - x -1 +
● L 1= lim f(x)=2(β+e - 1 + 1 )
x - 1 -
=2(β+e ) =2(β+1)
0
=f(- 1)

● L 2= lim f(x)
x - 1 +
α(x+1)
= lim +2
x - 1 + x+2-1

α(x+1)( x+2 +1)
= lim +2
x - 1 + ( x+2-1)( x+2 +1)

α(x+1)( x+2 +1)
= lim +2
x - 1 + x+2-1
α(x+1) ( x+2 +1)
= lim +2
x - 1 + x+1

= lim α( x+2 +1)+2 = α( -1+2 +1)+2= 2(α+1)
x - 1 +
άρα
L 1= L 2`2(β+1)=2(α+1)`α+1=β+1`α=β (1)

Αφού η C f διέρχεται από το σημείο Μ(2, 11), τότε f(2)=11 και

α(2+1) 3α
f(2)= 11 ` +2= 11 ` +2= 11 `3α= 9`α= 3 (2)
2+2-1 1
Από (1) και (2)
α=β=3

Τακης Τσακαλακος Κερκυρα 2017