Page 367 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 367

 Όταν υπάρχει πλάγια η οριζόντια ασύμπτωτη, τότε αυτή είναι
μοναδική

 Αν η γραφική παράσταση της f έχει πλάγια ασύμπτωτη, τότε
δεν θα έχει οριζόντια και αντίστροφα

 Μπορεί η γραφική παράσταση της f να έχει κατακόρυφες
α σ ύμπτωτες και οριζόντια η πλάγια ασύμπτωτη

 Δεν έχουν ασύμπτωτες:
 Οι πολυωνυμικές συναρ-
τήσεις με βαθμό ν 2

 Οι ρητές συναρτήσεις που
η διαφορά βαθμών αριθ-
μητή και παρονομαστή ε ί -
ναι μεγαλύτερη ή ίση μ ε 2

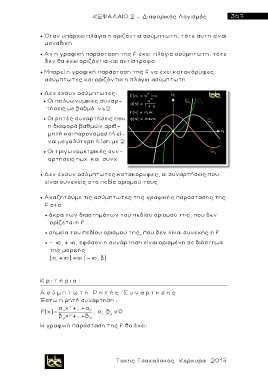
 Οι τριγωνομετρικές συν-
αρτήσεις η μ x και συνx

 Δεν έχουν ασύμ π τωτες κατακόρυφες, οι συναρτήσεις που
είναι συνεχ ε ίς στο πεδίο ορισμού τους

 Αναζητούμε τις ασύμπτωτες της γραφικής παράστασης της
f στα
 άκρα των διαστημάτων του πεδίου ορισμού της, που δεν

ο ρ ίζεται η f
 σημεία του πεδίου ορισμού της, που δεν είναι συνεχής η f

 - , + , εφόσον η συνάρτηση είναι ορισμένη σε διάστημα
της μορφής
(α, + ) και (- , β)

Κ ρ ι τ ή ρ ι α :

Α σ ύ μ π τ ω τ η Ρ η τ ή ς Σ υ ν ά ρ τ η σ η ς
Έστω η ρητή συνάρτηση :
ν
α x +... +α
f(x)= ν 0 , α × β 0
β x +... +β ν μ
μ
μ 0
Η γραφική παράσταση της f θα έχει:

Τακης Τσακαλακος Κερκυρα 2017