Page 369 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 369

 Στη πρώτη παρατηρήσ η
" Η γραφική παράσταση
της f τέμνει το πολύ σε
ένα σημείο τη κατακόρ υ -
φη ασύμπτωτη" ισχύει, α-
φ ο ύ σε διαφορετική περί-
πτωση η f δεν θα α π οτ ε -
λ ο ύσε συνάρτηση

(θα υπήρχε χ 0 Α f με πε-
ρισσότερες ή ίσες με 2
τιμες).
παράδειγμα, η συνάρτηση
με τύπο
1 , χ> 1
f(x)= χ-1
χ+1 , χ 1
με κατακόρυφη ασύμπτωτη την ευθεία χ=1 και το σημείο
Α(1,2) α ν ήκει σ'αυτήν, αφού
 lim f(x)= +
x 1
 f(1)=1 1 2

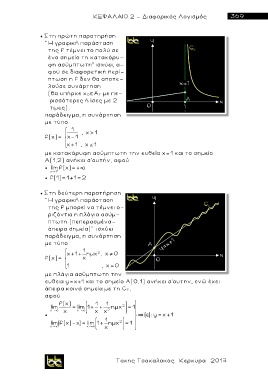
 Στη δεύτερη παρατήρηση
" Η γραφική παράσταση
της f μπορεί να τέμνει ο-
ριζόντια η πλάγια ασύμ-
πτωτη (πεπερασμένα-
άπειρα σημεία)" ισχύει
παράδειγμα, η συνάρτηση
με τύπο
1
1 ημχ , χ 0
2
f(x)= χ
1 , χ 0

με πλάγια ασύμπτωτη την
ευθεια y=χ+1 και το σημείο Α ( 0,1) ανήκει σ'αυτην, ε ν ώ έχει
άπειρα κοινά σημεία με τη C f,
αφού
f(x) 1 1
lim = lim 1 ημχ 2 = 1
x x χ χ 2
 ( ): y x 1
lim(f(x) ) lim 1 1 ημχ 2 1
x x χ

Τακης Τσακαλακος Κερκυρα 2017